VIDEO TRANSCRIPT

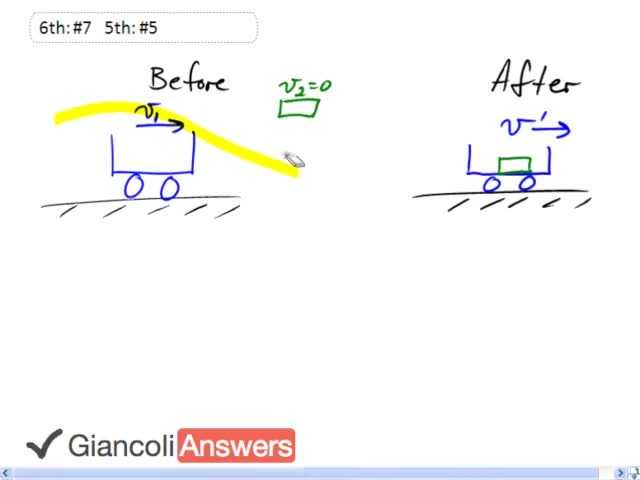
So this railroad car is initially travelling along the track with a speed ‘v1’ and there's this load waiting to be dropped into he car and it’s not moving initially. So the total momentum in the before scenario is just the momentum of the cart, the load has no momentum because it’s not moving at all to begin with. After it’s dropped into the cart the total momentum will be the one object with both the railroad car and the load, that total mass will be moving with some common velocity ‘v`’ and so that will be the momentum after. Let’s write down some formulas to talk about this. The total momentum before a collision or event is equal to the total momentum afterwards and we’ll recognize that ‘v1`’ and ‘v2`’ are the same so let’s just call them ‘v`’. Also ‘v2’, the initial velocity of the load is zero and so the term ‘m2’ times ‘v2’ disappears and our equation is: ‘m1’ times ‘v1’ equals the mass of the railroad car ‘m1’ plus the load ‘m2’ times ‘v`’ then we’ll solve for ‘v`’ by dividing everything by ‘m1’ plus ‘m2’ so that gives: ‘v`’ is ‘m1’ times ‘v1’ divided by ‘m1’ plus ‘m2’ and we’ll substitute in numbers: twelve thousand six hundred kilograms is the mass of the railroad car times its initial velocity of eighteen point zero meters per second divided by twelve thousand six hundred kilograms plus the mass of the load, five thousand there hundred and fifty kilograms giving us a ‘v`’ after the load is dropped on the car of twelve point six meters per second. In the 5th Edition the railroad car is twelve thousand five hundred kilograms and the load that's dropped into it is five thousand seven hundred and fifty kilograms meaning the 5th Edition answer for ‘v`’ will be twelve point three meters per second.