VIDEO TRANSCRIPT

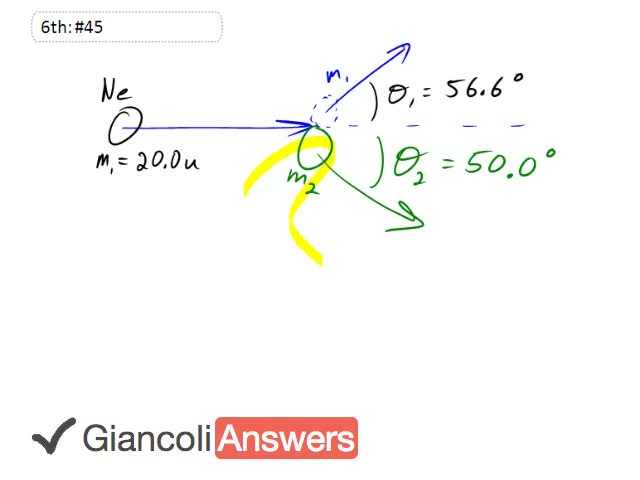
We have a neon nucleus coming in to impact this other nucleus which is initially at rest and the neon deflects at an angle of fifty six point six degrees after collision and the other unknown nucleus deflects at fifty degrees after the collision. It’s a perfectly elastic collision so that means we can write down the conversation of energy which is ‘m1’ times ‘v1’ squared, that’s the initial kinetic, equals ‘m1’ times ‘v1`’ squared plus ‘m2’ times ‘v2`’ squared. The question in the text book gives us a hint that we should use the law of sines. So that means when we write our momentum conservation we’re not going to write it in terms of components, instead we’re going to write the momentum vectors in a single triangle. And that is to say that the momentum of the neon, let’s call this ‘m1’ times ‘v1`’ plus the momentum of the unknown nucleus, ‘m2’ times ‘v2`’ which all adds up to the initial momentum of the neon as it was incoming, ‘m1’ times ‘v1’. This is another way to say that momentum is conserved because what we’re really saying is that the two momentum vectors after collision have to add up to the momentum vector before the collision. Now let’s get some angles on to his picture: we know that this angle is fifty five point six degrees, and imagining a horizontal line here, this one is ‘θ2’ which is fifty degrees and this bit here is also fifty five point six degrees, and then one eighty minus fifty five point six and also minus fifty gives us this angle here which is seventy four point four degrees. The total angles in the triangle have to add up to one hundred and eighty, meaning the left over amount is fifty degrees for that angle. So now we know every angle and we can relate the sides using the law of sines which is to say that this side divided by the sine of the opposite angle which is fifty five point six is going to equal any other side divided by the sine of its opposite angle. So we can say: ‘m1’ times ‘v1’ divided by sine of seventy four point four degrees equals ‘m2’ times ‘v2`’ divided by the sine of fifty five point six degrees, which is ‘m1’ times ‘v1`’ divided by the sine of fifty degrees. We have our conservation of energy equation and we want to find ’m2’, if we substitute for ‘v1`’ and replace it with ‘m1’ times ‘v1’ type terms they’ll all cancel and we’ll get rid of all our variables. So from the law of sines we can say that ‘v1`’ equals ‘v1’ times sine fifty divided by sine seventy four point four degrees and then divided by ‘m1’ as well. So ‘v1`’ is ‘v1’ sine fifty over sine seventy four point four zero. ‘v2`’ is ‘m1’ over ‘m2’ times ‘v1’ times sine fifty five point six divided by sine seventy four point four. We then substitute into the energy equation for ‘v1`’ and ‘v2`’, so it says: ‘m1’ times ‘v1’ squared equals ‘m1’ times ‘v1’ sine fifty over seventy four point four degrees all squared plus ‘m2’ times ‘m1’ times ‘v1’ sine fifty five point six divided by ‘m2’ times sine seventy four point four all squared. Simplifying and factoring out common factors: one equals sine squared fifty divided by sine squared seventy four point four plus ‘m1’ sine squared fifty five point six divided by ‘m2’ times sine squared seventy four point four. Solving for ‘m2’: ‘m2’ times sine squared seventy four point four equals ‘m2’ times sine squared fifty plus ‘m1’ sine squared fifty five point six, factoring out the ‘m2’s: ‘m2’ times sine squared seventy four point four minus sine squared fifty equals ‘m1’ sine squared fifty five point six. Dividing by sine squared seventy four point four minus sine squared fifty gives us: ‘m2’ equals ‘m1’ sine squared fifty five divided by sine squared seventy four point four minus sine squared fifty. ‘m1’ is twenty point zero atomic units, so doing the calculation: ‘m2’ is thirty nine point nine atomic units.