VIDEO TRANSCRIPT

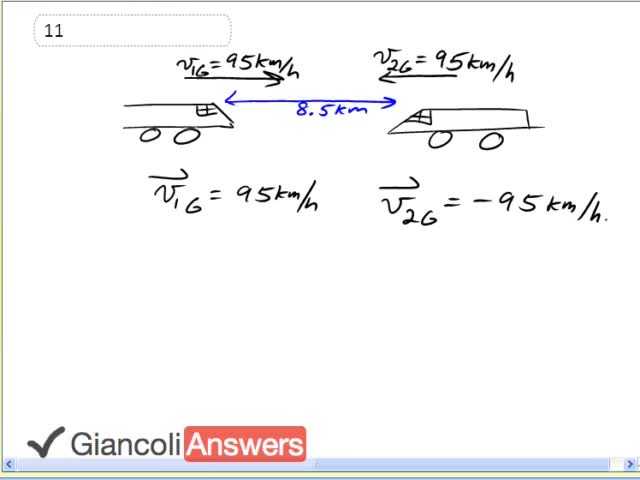
These trains are approaching each other with speeds of ninety five kilometers an hour and they're eight and a half kilometers apart. We’re going to answer this question by figuring out what is the relative velocity of train two with respect to train one. The velocity of train one is ninety five kilometers an hour because we’ll take to the right as the positive ‘x’ direction and the velocity of train two is negative ninety five kilometers an hour. To find the velocity with which train two is approaching train one is another way of saying relative velocity of train two with respect to one, which is: ‘v2g’ minus ‘v1g’ which is negative ninety five kilometers per hour minus positive ninety five kilometers per hour which equals negative one hundred and ninety kilometers an hour. So train two appears to be approaching train one at a relative velocity of negative one hundred and ninety kilometers an hour. Using that we’ll find the time it takes to close this gap of eight and a half kilometers between them. This is a general way of answering a question like this. You could’ve said that both trains will each cover half the distance and figure it out from there, but I’m showing you this method because it’s general, you don’t need to figure out what fraction of the total distance each train will cover. It will work for any given velocities and any separation distances. So train two is going to displace towards train one, that’s negative eight and a half kilometers to the left, and then it’s relative velocity is negative one hundred and ninety kilometers per hour so our answer is: it’s going to take zero point zero four four seven hours or two point seven minutes.