VIDEO TRANSCRIPT

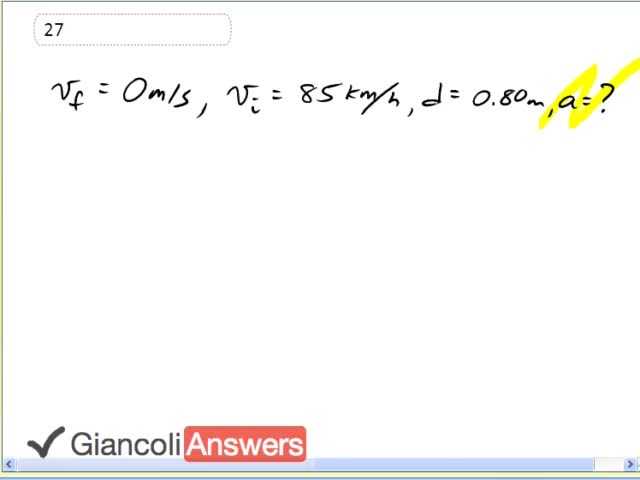
Our job is to figure out what is the acceleration in the units of ‘g’s for a car that hits a tree and comes to stop within zero point eight meters, that’s how much the front of it compresses given an initial speed of the car of eighty five kilometers an hour. Our first order of business will be to take the units of the initial speed and change it into meters per second, so eighty five kilometers an hour times one hour for every three thousand six hundred seconds times one thousand meters for every kilometer or you can think of this as dividing by three point six, that’s twenty three point six one one meters per second. Then we’ll use the formula ‘vf2’ equals ‘vi2’ plus two ‘a’ times ‘d’ and we’re solving for ‘a’. We can get rid of ‘vf’ since it comes to a stop it’s zero. We’ll subtract ‘vi2’ from both sides so we get 2 ‘a’ times‘d’ equals negative ‘vi2’ and then we’ll divide both ides by 2‘d’ because we’re solving for ‘a’ which is negative initial speed squared divided by two times ‘d’ which is negative twenty three point six one one meters per second all squared divided by two time zero point eight meters that gives negative three hundred and forty eight point four meters per second squared as the acceleration. We’ll convert that to ‘g’s now, acceleration is: negative three hundred and eighty four point four meters per second squared times one ‘g’ for every nine point eight meters per second square which is negative thirty five point five five ‘g’ which in two significant figures is negative thirty six ‘g’s which is close to being lethal; according to Wikipedia negative fifty ‘g’s is the threshold when serious injury or worse can happen. Ninety kilometers per hour is the official speed for the 5th Edition, that’s a speed of twenty five point zero meters per second, substituting that here acceleration is negative three hundred and ninety point six and the number of ‘g’s is negative forty ‘g’s.