VIDEO TRANSCRIPT

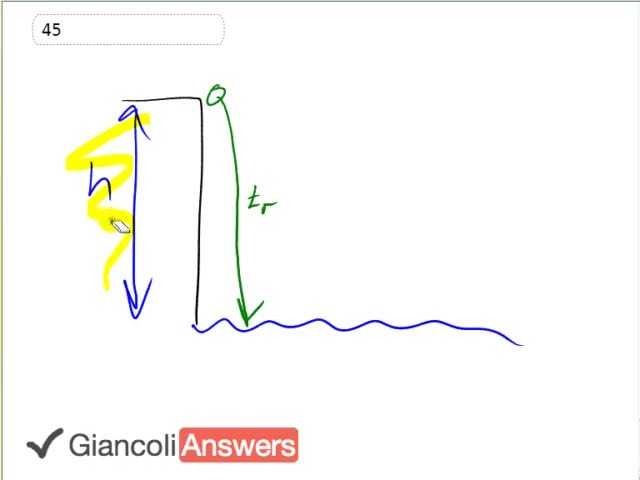
This rock is dropped from the top of a cliff which has some height ‘h’ that we’ll have to figure out and it takes some time ‘tr’ to get to the water. And we don’t know what that time is but we do know the total time for the rock to fall and for the sound to come back up, so there’s some time ‘ts’ for the sound to get from the water where the splash occur back up to the person who is listening. We know that the total of ‘tr’ for the rock to fall plus ‘ts’ for the sound to get back to the top is three point two seconds. Now we’re going to create a system of equations for the height that we can then substitute stuff into in order to answer our question. So we’re going to say height on the one hand is: one half ‘a’ times ‘tr2’ so the rock is accelerating downwards and this is the formula for the distance that it travels assuming that it has an initial speed of zero which it does, and we also know the height can be expressed as: the speed of sound multiplied by the amount time the sound takes to travel. So our strategy here is we know we want to find height so let’s make as many equations as we can for it and then we’ll see that we can actually combine these equations to answer the question. We can substitute for ‘ts’ and instead write: ‘ts’ equals three point two seconds minus ‘tr’ and then we’ll equate these two equations because they're both equal to height so that means they must be equal to each other so have one half ‘a’ times ‘tr2’ equals the speed of sound ‘vs’ times three point two seconds minus ‘tr’. I did two things there: equated the two equations and I substituted for ‘ts’. So we have a quadratic equation for ‘tr’, so we have one half ‘a’ times ‘tr2’ equals three point two seconds times ‘vs’ minus ‘tr’ times ‘vs’ and then bringing everything together so it has the usual form for a quadratic equation: one half ‘a’ times ‘tr2’ plus ‘tr’ times ‘vs’ minus three point two ‘vs’ equals zero. Simplifying and substituting in numbers we have: one half times nine point eight meters per second squared times ‘tr2’ plus the speed of sound three hundred and forty meters per second squared times ‘tr’ minus three point two times three hundred and forty meters per second equals zero. The quadratic equation is four point nine ‘tr2’ plus three hundred and forty ‘tr’ minus one thousand and eighty eight equals zero. Using the quadratic formula to solve that, and if you have questions about how leave a comment below this video, the time that the rock spend falling is three point zero six four six seconds. This means that the height of the cliff which we know from the beginning of this question is one half ‘a’ times ‘tr2’ is: one half times nine point eight meters per second squared times three point zero six four six seconds squared which is forty six meters. In the 5th Edition we have a time of three point four seconds as the total, so substituting gives the time for the rock to fall as three point two four seven nine seven seconds an the 5th Edition answer is that the height of the cliff is fifty two meters.