VIDEO TRANSCRIPT

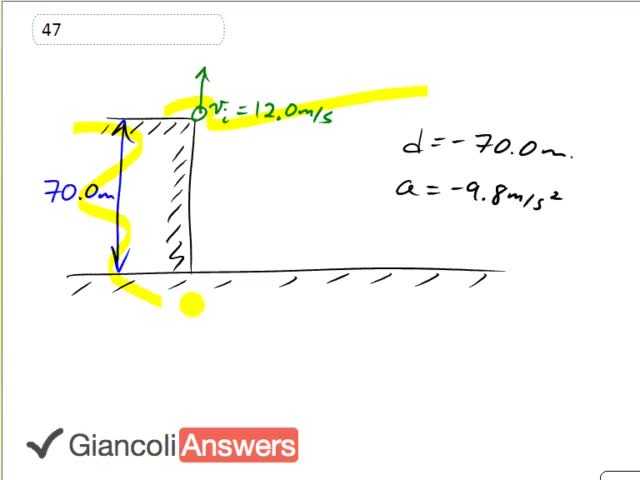
The stone initially has a velocity upwards of twelve meters per second from a cliff that’s seventy meters high and it’s going to hit the ground sometime later and our job is to figure out how much later and secondly to figure out its speed when it hits the ground and then figure out the total distance travelled. The displacement is going to be negative seventy meters because it’s downwards and the acceleration due to gravity is negative nine point eight meters per second squared. Part a we’ll solve with the equation: ‘d’ equals ‘vi’ times ‘t’ time plus one half ‘t’ times ‘t’ squared and we’ll solve this for ‘t’ by writing it in the form of a quadratic equation so one half ‘a’ times ‘t’ squared plus ‘vi’ times ‘t’ minus ‘d’ equals zero. Substituting in numbers, that’s one half times negative nine point eight meters per second squared times ‘t’ squared plus positive twelve point zero meters per second since it’s initially going upwards minus negative seventy meters displacement downwards equals zero so that’s negative four point nine ‘t’ squared plus twelve ‘t’ plus seventy equals zero and if you have any questions about how to solve this quadratic equation let me know, it’s the quadratic formula. You can leave a comment below the video and I’ll answer your questions. So that five point one nine seven five seconds which we’ll write as five point two zero seconds later the stone will hit the bottom of the cliff. Part b, we’re going to figure out its speed when it hits the bottom of the cliff so we’ll use ‘vf2’ equals ‘vi2’ plus two ‘a’ times ‘d’. Notice that I’m choosing to not use this time in part b because it’s nice to use original data in your work instead of stuff that you’ve calculated because maybe there's a mistake in this calculation, so use original data wherever possible. ‘vf’ is the square root of positive twelve point zero meters per second squared plus two times negative nine point eight meters per second squared times negative seventy meters and that gives a speed of thirty eight point nine three five eight which we’ll right as thirty eight point nine meters per second which will be the stone’s sped when it hits the bottom of the cliff. The total distance travelled is the question now. We’ll again use the equation ‘vf2’ equals ‘vi2’ plus two ‘a’ times ‘d’ but instead of ‘d’ I’m going to call it ‘hmax’. This is not going to give us the final answer from this particular equation, we’re going to solve this for ‘hmax’ and what I mean by that is this height from the starting position to the very top of its peak that’s ‘hmax’ so we’ll multiply that by two since it’s going to go up that distance and then back down and then add to that the seventy meter height of the cliff. The final velocity is zero at the very top of its peak and that means ‘hmax’ is negative ‘vi’ squared over two ‘a’ which is negative twelve meters per second squared divided by two times negative nine point eight meters per second squared and that’s seven point three four six nine meters. And so the total distance covered which is the answer to our question is: two times ‘hmax’ plus seventy meters which is two times seven point three four six nine meters plus seventy which gives eighty four point seven meters as the total distance covered by the stone. In the 5th Edition the numbers are slightly different and we have seventy five meters instead of seventy meters, the time in the 5th Edition is five point three two seconds. In part b we have negative seventy five meters giving us a final velocity in the 5th Edition of forty point two meters per second and then we have to add seventy five meters to the doubled maxed height to give an answer of eighty nine point seven meters as the total distance travelled.