
In order to watch this solution you need to have a subscription.
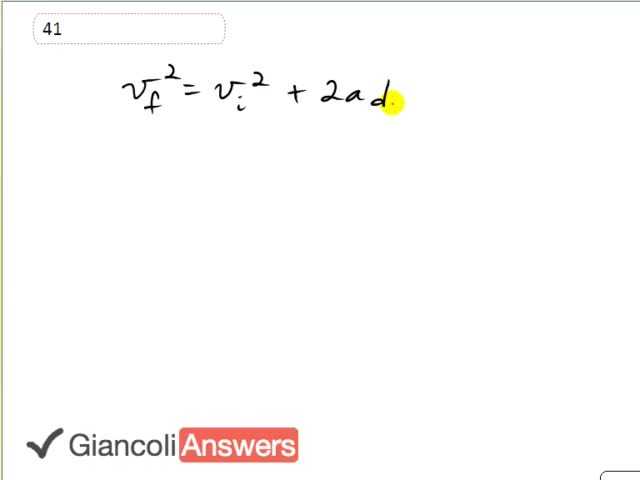
The formula: final speed equals the initial speed squared plus two ‘a’ times ‘d’ will help us answer this question. We’re going to solve for ‘vf’ assuming that ‘d’ is zero if a guy throws the ball up and then it comes right back down to the same position that means its displacement is zero which means the entire term two ‘a’ times ‘d’ is zero and for that reason the final speed ‘vf’ squared equals the initial velocity squared and taking the square root of both sides we have: ‘vf’ equals plus or minus ‘vi’ and the plus or minus means ‘vf’ equals positive ‘vi’ at the very initial moment, the initial speed there, and then some time later we get the second solution and we have the final velocity is in the opposite direction but same magnitude as the initial velocity.
How can the final velocity be equal to both the positive and negative initial velocity? Shouldn't the final velocity be only equal to the negative initial velocity due to direction? Thank you.
Hi elizabeth, thanks for the question. The formula is more generic than you're imagining. I think what you have in mind is that at the time when the ball has returned to the thrower's hand, and that's true. But this formula works for all times when displacement is zero (), and there's one other time when that's the case, namely, in the beginning! This "in the beginning" solution is kind of trivial since it's so obvious that the final velocity after basically no time has elapsed is the same as the initial velocity. This is what the solution is telling us, that there is a moment when the final velocity is equal to the positive of the initial velocity, and it's our job to make the physical interpretation of that mathematical solution to understand that it's referring to the moment when the ball is launched. The formula gives all solutions when the displacement is zero, and there are two moments when that's the case: initial launch, and the much later return to the hand.
Hope that helps,
Mr. Dychko