VIDEO TRANSCRIPT

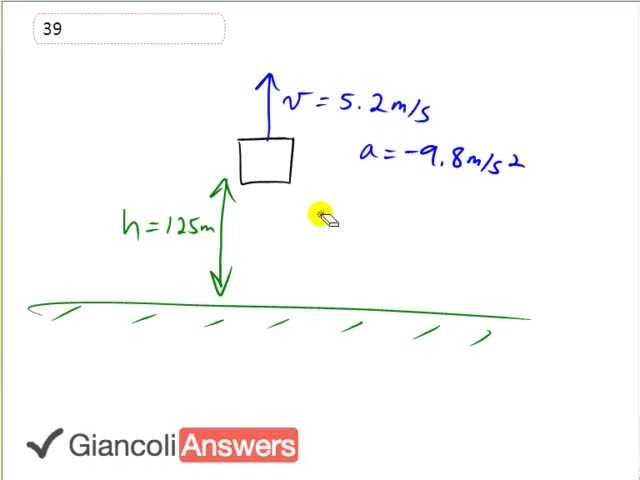
This package which is dropped from the helicopter at a height of one hundred and twenty five meters of the ground is initially going upwards with the helicopter at a speed of five point two meters per second. Its acceleration after it leaves the helicopter will be acceleration due to gravity, nine point eight meters per second squared down and our job is to figure out how long it will take to hit the ground. We’re going to use the formula: ‘d’ equals initial velocity ‘vi’ times time ‘t’ plus one half ‘a’ times ‘t’ squared. This is a quadratic equation that we’ll solve using the quadratic formula for ‘t’: subtracting ‘d’ from both sides we’ll have one half ‘a’ times ‘t’ squared plus ‘vi’ times ‘t’ minus ‘d’ equals zero, that’s the usual form for a quadratic equation. Substituting in numbers we have one half times negative nine point eight meters per second squared times ‘t2’ plus positive five point two meters times ‘t’ minus negative one hundred and twenty five equals zero. The first negative sign is because the package will be displacing one hundred and twenty five meters downwards. The other negative sign resulted from the algebra of subtracting ‘d’ form both sides so we have negative four point nine zero ‘t2’ plus five point two zero ‘t’ plus one hundred and twenty five equals zero and the quadratic equation gives you an answer of ‘t’ equals five point six one seconds. If you want to know more about using the quadratic formula let me know in the comments below this video and I’ll give you some more pointers. In the 5th Edition the numbers are slightly different, initial speed upwards is five point five zero meters per second and an initial height of one hundred and five meters. So we’ll just substitute those numbers into our equation and we’ll get an answer of ‘t’ equals five point two two seconds to fall to the ground in the 5th Edition.