VIDEO TRANSCRIPT

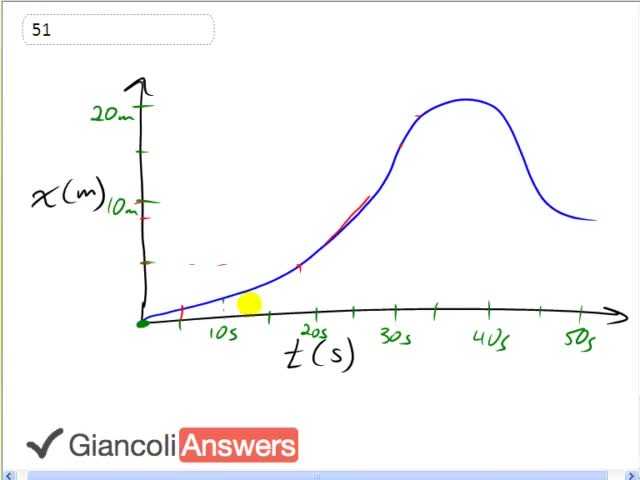
In order to say when the velocity is constant we need to find the points in this graph where the slope is constant because the slope of a position-time graph is velocity. And we’ll see that its approx constant up to about twenty two seconds before it starts to curve, so from zero to twenty two seconds we are going to say that the slope looks like it’s about constant. In that case the velocity is constant. For part b it asks: at what time is the velocity greatest? And so we are trying to find the region where the slope is the most steep, where it has the most rise for a given run. So that appears to be in the region from about twenty two to twenty nine seconds. In part c it asks: so what time is the velocity zero and that will be just at this particular instant there at the peak, this is where the object changes direction. Initially it’s going forwards as you can tell because the position is increasing and then at this point in time it’s not going anywhere because it’s about to start going backwards and you can tell it’s going backwards in this region because it’s position is going smaller, so from about twenty two back towards zero, it’s getting less and less far from the origin and this is the point where it starts to turn around, the velocity is zero there. And you can also say the slope of the tangent line is zero at that point, it would be another way of stating this answer. And slope of the tangent line being the instantaneous velocity at any time on a position-time graph. We’ll say that it’s about thirty seven seconds and does it go in one direction or both? Well, the answer is both as we have already said so it’s increasing its position here, positive velocity in other words and it’s decreasing its position here as you can see from a negative slope or a negative velocity. That’s for d as both.