
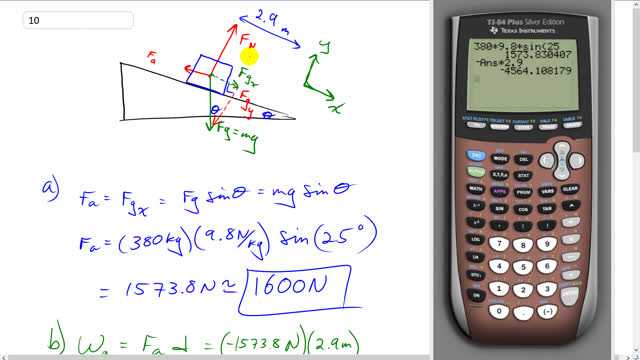
A 380-kg piano slides 2.9 m down a incline and is kept from accelerating by a man who is pushing back on it parallel to the incline (Fig. 6–36). Determine:
- the force exerted by the man,
- the work done on the piano by the man,
- the work done on the piano by the force of gravity, and
- the net work done on the piano. Ignore friction.

In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Here's a free-body diagram of the piano sliding down the ramp at constant speed. We have the applied force by the man going up the ramp equal to the component of gravity that's down along the ramp, F gx. And, we also have a normal force that doesn't really matter. I have moved my coordinate system so that it's tilted with the x-axis, along the ramp, positive down. And the first question is, "what is the applied force of the man?" Well, the applied force has to equal F gx in order to have constant speed down the ramp; no net force, in other words. And that's gonna be F g which is gravity mg multiplied by sin theta because this is the opposite leg of that triangle. So we have 380 kilograms times 9.8 newtons per kilograms times sin 25 gives about 1600 newtons. And the work done by the man will be the applied force times the displacement. But, in this case, we have to put a negative sign in front of the applied force because direction matters here and the force is up the ramp and so it's negative 1573.8 newtons and then times 2.9 meters. And I guess, technically, I should put a negative in front of that one too. So there we go. And that's negative 4600 joules. For the work done by gravity, the x-component of gravity is in the same direction as the displacement so that's what we wanna use for the gravity's force as the x-component of it and multiply and that's equal to the applied force, which we already know. And multiply it by the displacement along the ramp and we get the same answer but now it's positive because gravity is acting in the same direction as the displacement; they are both down the ramp. And the net force is zero so that means the net work done on this piano is also zero. You could have also argued that that work is the change in kinetic energy and since it's moving at constant speed, change in kinetic energy has to be zero. So that would be another way to say that net work is zero.
The answer at the top of the page says -1600N and I believe it should be a positive number (+1600N).
Hi msjmai, thanks for the comment. Since the coordinate system is defined as positive down the ramp, whereas the applied force is up the ramp, this makes the applied force is in the negative direction. The screenshot for the video shows +1600N at the particular moment the screenshot was taken, but at 1:16 in the video I mention that it should actually be negative.
Cheers,
Mr. Dychko