
What is the minimum work needed to push a 950-kg car 710 m up along a incline? Ignore friction.
In order to watch this solution you need to have a subscription.
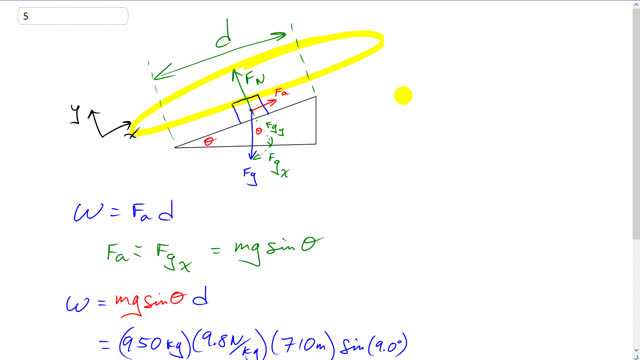
This is Giancoli Answers with Mr. Dychko. Here's a free-body diagram of this car being pushed up the ramp. The 710 meter, length of the ramp, refers to this length on the diagonal here and so it's being pushed along 710 meters from the start to the finish here. The applied force, since we are asked to find the minimum amount of work, the applied force is gonna have to equal the x-component of the gravity force; x-axis being along the ramp. If the applied force could be greater than that but then there would be some acceleration, and it doesn't have to be that any greater than this coz we are trying to find just, what is it, the minimum. So couldn't be any less than this component of gravity because then the car would accelerate down the ramp. Alrighty! So the work done by this applied force is gonna be the force multiplied by the displacement along the ramp, and those are parallel so there's no need to take angles into account there. The only place where an angle is considered is where we calculate the x-component of gravity because it's gonna be gravity, which is mg, multiplied by sin theta because this component is the opposite leg of this triangle and so we use sin theta times mg to get the applied force. And we substitute that in, for applied force here in, our work formula multiply it by the displacement and we get 950 kilograms times 9.8 newtons per kilograms times 710 meters times sin of 9 degrees, that gives 1.0 times 10 to the 6 joules.
Why don't you use cosine theta in the work formula at the very end of the problem if W=Fdcos(theta)? instead of just d (just displacement) in incline problems like this?
Hi lyonsca1,
Thanks for the question. I don't mean at all to contradict (which can also be written ). That formula means that you multiply the force by the displacement, then multiply by cosine of the angle between them. In this particular solution, the force and displacement are actually parallel. The force I'm referring to is the force applied by some person or machine to make the car move up the ramp at constant speed. This applied force is directed along the ramp, so it's parallel to the length of the ramp. This means . Since , it's common to not bother writing it at all, and to just write for the special case where , which is the case where the force and displacement are parallel, as they are in this problem.
The applied force, according to the diagram, is , where theta here is referring to the angle of the incline. That's confusing, since the "theta" in the formula you wrote is referring to something different: namely the angle between the applied force and the displacement. If I were to write things out completely, using numbers in place of the angles, it would be , where I added the to try and be clear that that angle is the one in the formula, not the used to calculate the component of gravity along the incline.
Hope that helps,
Mr. Dychko
Why is Fa applied force equal to Fg gravitational force?