
In a certain library the first shelf is 15.0 cm off the ground, and the remaining four shelves are each spaced 38.0 cm above the previous one. If the average book has a mass of 1.40 kg with a height of 22.0 cm, and an average shelf holds 28 books (standing vertically), how much work is required to fill all the shelves, assuming the books are all laying flat on the floor to start?
In order to watch this solution you need to have a subscription.
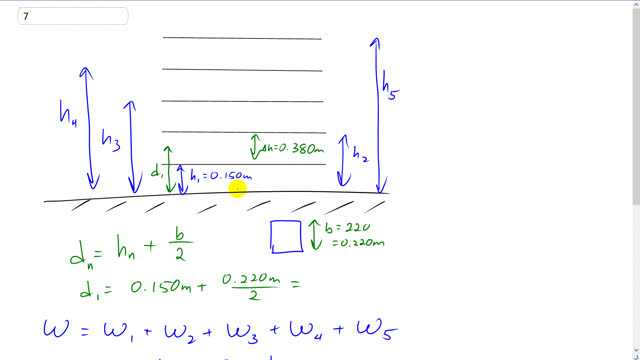
This is Giancoli Answers with Mr. Dychko. So we assume that the book's are lying flat on the floor, to begin with. And to figure out, how much work it is to lift one book up, we need to know how much we are gonna raise up the book's center of mass? So, center of mass of a book is in the middle of the book say. It's gonna have a uniform mass distribution, paper's all the same density everywhere. And so, the center of mass is gonna go from the floor level up to the shelf plus half the height of the book. So, that's why I have b over 2 here; b is the 22 centimeter height of the book and that's 0.220 meters. And then half of that, above the shelf is where the center of mass is gonna get positioned. So, the height of the center of mass goes up but then is the height of the shelf, 0.15 meters for this first shelf, plus the point 0.22 meter height of the book divided by 2. And, what did that work out to? Well, I guess we can calculate it by 0.15 plus 0.22 over 2, which is 0.11 and we get 0.26 meters. So, that's the first height. And then we have 28 books there so we'll have to multiply that by 28 to get the total amount of work to put books on the first shelf. And then we have shelf 2, 3, 4 and 5 as well to consider so the total work done will be the work to fill shelf 1 then the work to fill shelf 2 and so on up to shelf 5. So, the work to fill shelf 1 is 28 books times the weight of a book because the upwards force is gonna equal the weight, in order to get the minimum amount of work needed to to fill the shelf. I mean, you could lift it up with more force than the weight but then you would be doing extra work for no extra need, no reason. So, and then plus 28 books times mg times the height of the center of mass on the second shelf, and so on in all 5 books. Now, each of these work terms is gonna have 28mg multiplied by the height of center of mass. And, so we can factor out that 28mg from each of these terms. So, it's 28mg times d 1 plus d 2 plus d 3 plus d 4 plus d 5. And so we have 28 times 1.40 kilograms times 9.8 newtons per kilogram times 0.26 meters, for the first shelf; and then add 0.38 meters because that's the separation between shelves to that for the second shelf so you get 0.64 meters; and then plus 0.38 plus 0.38 plus 0.38 and you get all these different heights. Add them together, multiply by these factors in front and you get 1960 joules is the total amount of work to put all the books on the shelf.