A grocery cart with mass of 16 kg is being pushed at constant speed up a $12 ^\circ$ ramp by a force $F_P$ which acts at an angle of $17 ^\circ$ below the horizontal. Find the work done by each of the forces $(m\vec{g}$, $\vec{F}_N$, $\vec{F}_P)$ on the cart if the ramp is 7.5 m long.

VIDEO TRANSCRIPT

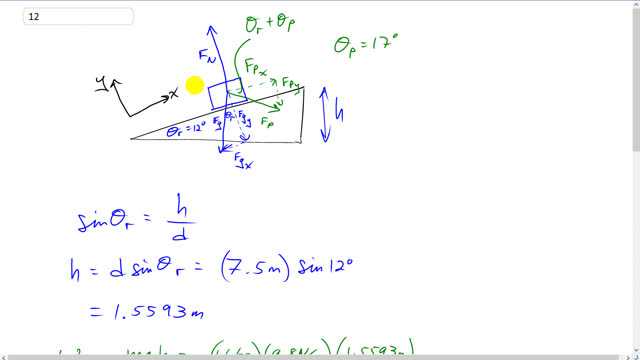
This is Giancoli Answers with Mr. Dychko. Here's a free-body diagram on this grocery cart; we have gravity straight down. It's going up this ramp, inclined at 12 degrees. There's an applied force at an angle of 17 degrees below horizontal although it turns out that we are not gonna actually gonna use that number anywhere in the calculations and there's a normal force perpendicular to the ramp surface. So the work done by the normal force is a first thing to get out of the way; it's a zero because the grocery cart's displacement is up the ramp and it's perpendicular to the normal force. So there's no component of the normal force and the direction of displacement, no parallel component in other words, and so there's no work done by the normal force. Let's calculate the work done by gravity so gravity is straight down and the displacement is along the ramp, in the positive x-direction. And we'll find the component of the displacement that is parallel to the weight. So, that would be the vertical height. And so sin Θ r; Θ r is the incline of the ramp, equals opposite h over d, which is the length of the ramp, opposite over hypotenuse. And we can solve for h by multiplying both sides by d. And we get h is 7.5 meters times sin 12 degrees, which is 1.5593 meters vertical component to its displacement. So, we'll multiply that by gravity because now, you know, we have to have either the component of the displacement is parallel to the force or the component of the force parallel to the displacement. Either way, as long as you have parallel things that you are multiplying together, you can go right ahead to calculate work. So, we have putting a negative sign in front of that because the displacement is upwards and the force is downwards and so they are opposite direction so that means you have a negative, it's negative 16 kilograms times 9.8 newtons per kilogram times 1.5593 meters which gives about negative 240 joules of work done by gravity on the grocery cart. Now for the work done by the person, we have to take their x-component of their force, which is along the ramp here and multiply that by the displacement along the ramp. So, the x-component of this applied force must be equal to the x-component of gravity because this grocery cart is going at constant speed and so the x-component of gravity is mg times sin Θ r because this is the opposite leg of this gravity-force triangle and that's what we say here - F P x equals F g x and that's mg sin Θ r. So, we substitute, in place of, F P x, applied force by the person on the grocery cart in the x-direction is mg sin Θ r, which we write here times d. And so the work done by the person is 16 times 9.8 times sin 12 times 7.5, which again is 240 joules and this time it's positive because the applied force is in the same direction as the displacement. And no surprise that this is equal and opposite sign to this one because the net work on this grocery cart should be zero since there is no change in kinetic energy. And again, the normal force does zero work since there's no component of the normal force parallel to the displacement.