
A vertical spring (ignore its mass), whose spring constant is 875 N/m, is attached to a table and is compressed down by 0.160 m.
- What upward speed can it give to a 0.380-kg ball when released?
- How high above its original position (spring compressed) will the ball fly?
In order to watch this solution you need to have a subscription.
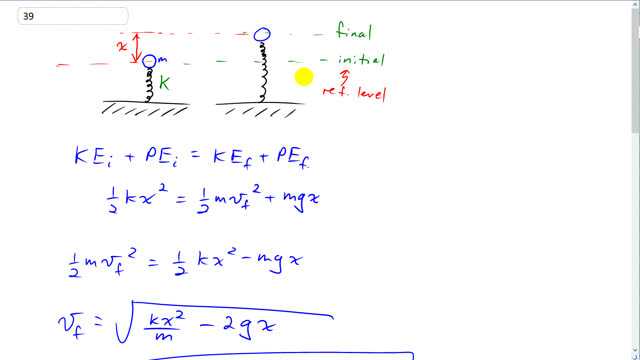
This is Giancoli Answers with Mr. Dychko. As usual, we equate the total initial energy with the total final energy and the tricky part is always figuring out how do you calculate these energies? So, initially, we'll take this to be the reference level when the spring is fully compressed, in which case, there will be no gravitational potential; there's no kinetic because it's at rest here and so it's all elastic potential energy - one-half times spring constant times the amount the spring is compressed, squared. And that will equal the kinetic energy it has at this final position when this spring is fully uncompressed and is just about to launch off the spring and it will also have some potential energy there due to gravity because it will be above this initial reference level. And it will be an amount x above the reference level, where x is the amount the spring is compressed. So, we have to solve this for v f. So, we'll take this term to the left side which makes it minus and then we have this line here, and then we'll multiply both sides by 2 and divide by m. And so we have, we have k x squared over m and then minus 2gx. And take the square root of both sides to solve for v f and we get the final speed is square root of 875 newtons per meter times 0.16 meter squared over 0.38 kilograms minus 2 times 9.8 meters per second squared times 0.16 meters which gives 7.47 meters per second will be the launch speed of the ball off the spring. And then we are asked, how high will it go? And so, we'll take the initial moment to be the same where the ball is initially at rest, on a compressed spring. But now the final moment will be when the ball is at its maximum height and at this final moment, it will have no kinetic energy because it's not moving at the maximum height. And it will have just gravitational potential; no elastic potential energy because the spring is totally uncompressed at this point. So it's potential energy, mgh, where h is measured above this reference level which is the initial position of the ball when the spring is fully compressed. And we'll solve this for h by dividing both sides by mg. And we have h is 875 newtons per meter—spring constant— times 0.16 meters squared— compression of the spring— divided by 2 times 0.38 kilograms times 9.8 newtons per kilogram which gives 3.01 meters maximum height above the initial compressed point, where it started.
Why is there no gravitational potential energy when the spring is compressed?
Just to clarify, I'm referring to part (b). Thanks!
Hi nschidlowsky, thanks for the question. You mention referring to part b), but the concept is also applies to part a) as well. Let's clarify one thing about gravitational potential energy: an absolute value never exists, but rather you can only ever calculate a difference in gravitational potential energy between two heights. Instead of saying "Gravitational Potential Energy", we should always be saying "Difference in Gravitational Potential Energy between the final position and the reference level", but that's too much to say, so we say "Gravitational Potential Energy" for short. When using the typical formula , where is the height above the ground, this is actually a calculation of the difference in potential energy between the ground (the ground is called the reference level in this case) and the position meters above the ground. In this particular video, instead of comparing to the ground, I calculated the gravitational potential between the final height and the initial height of the ball on the compressed spring. The initial position of the ball on the compressed spring is the reference level. That means the height of the ball initially is zero meters above the reference level, so is zero, and so there's no "gravitational potential energy".
Taking the reference level to be at the initial height of the compressed spring is strategic since it eliminates some variables: it means there is no gravitational potential energy term on the "initial" side of the energy conservation equation. There only exists elastic potential energy.
Hope this helps,
Mr. Dychko
I understand now. Thank you for your help!
For part b why can't you use the initial kinetic energy of the ball using the velocity you found from part to find the potential energy (mgh) and then solve for h? Why do you need to use the potential energy of the spring?
Just for clarification the way I thought it would be was KEi = PEf and both energies were referring to the energy of the ball.
Hi poojamukund10, thanks for the question. The tricky part is in the meaning of "h". You could do what you're suggesting, and calculate "h" to be the height that gives an amount of potential energy that is equivalent to the kinetic energy that the ball has when it is at the tip of the extended spring, but in this approach "h" will be the height above the extended spring, not the height above the initial starting point. As an interesting exercise (I haven't tried this, but it should work), why not add the answer for "h" in your approach to the amount by which the spring was compressed () and see if you get the same answer? Let me know how it goes.
All the best,
Mr. Dychko