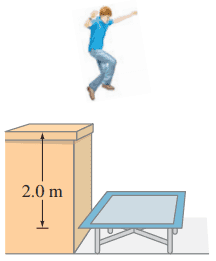
A 62-kg trampoline artist jumps upward from the top of a platform with a vertical speed of 4.5 m/s.

VIDEO TRANSCRIPT

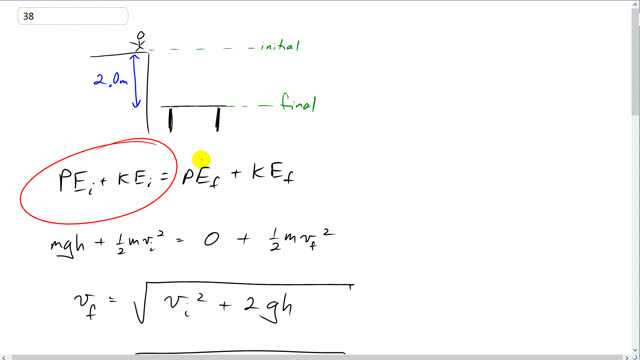
This is Giancoli Answers with Mr. Dychko. This trampoline artist starts at an initial positon 2 meters above the trampoline and the total kinetic plus potential energy they have at this initial position equals the total kinetic and potential energy they have at this final position, when they just begin hitting the trampoline. So initially, they have a potential energy of mgh; we'll take this final position to be the reference level so they have some height above that reference level equal to h, 2 meters. And they have some speed, one-half m v initial squared. And that equals the final potential energy which we will take to be zero since the final position is at the reference level. And then plus some one-half m v f squared, kinetic energy they have. And we'll solve for v f by dividing everything by m, multiply both sides by 2 and you get 2 times gh and plus v initial squared and we'll take the square root of both sides to solve for v f. And so v final is square root of 4.5 meters per second— initial speed—squared plus 2 times 9.8 meters per second squared times the two meter height above the trampoline, which gives 7.7 meters per second, just before they hit the trampoline. And then after hitting the trampoline, they are gonna squish the trampoline down, some distance x, and in this equation now, we are gonna be talking about initial and final total energy. We are going to take the initial point to be just when they begin hitting the trampoline. That was what we considered the final point a moment ago but now we are calling that our initial point. And then the final point will be when the trampoline is fully compressed and they come to a stop, at this position here and we are gonna take the final position to be the reference level again. So, initially, they do have some potential energy. At this location in part (a), they had no potential energy because that position at the top of the trampoline was our reference level. But now since the reference level has been moved down here to where this trampoline is fully compressed, they do have some potential energy here. And so that's equal to mg times this distance, x, above the reference level. And they have some kinetic energy as well; one-half v initial squared where their initial speed up here is this - final speed from part (a). And after this trampoline is fully compressed, they have no kinetic energy because they come to a stop and all the energy has been turned into elastic potential energy. And they have no gravitational potential energy because the final position is the reference level and they are zero meters above that reference level. So, we are gonna move everything to one side; take this to the right, take this to the right and they both become negative, switch the sides around and we have this. It's gonna be a quadratic equation then we'll have to use a quadratic formula to solve it. We have a spring constant of 5.8 times 10 to the 4 newtons per meter that gets divided by 2 times this amount of trampoline compression, x, squared minus 62 kilograms times 9.8 newtons per kilogram times x minus the mass times their speed at the beginning of compressing the trampoline. That gets squared, divided by 2; all that equals zero and this is a quadratic equation. And so we'll plug into our quadratic formula and you can see on the calculator what that looks like. Make sure you have all your bracket matching correct. And you get about 0.26 meters as the amount of compression of the trampoline.