
A novice skier, starting from rest, slides down an icy frictionless incline whose vertical height is 105 m. How fast is she going when she reaches the bottom?
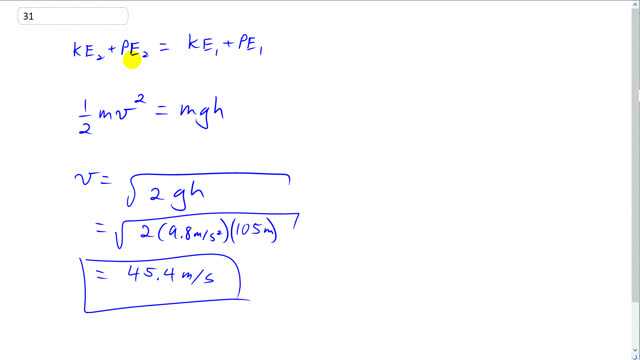
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The total of the kinetic and potential energy at the top of the ski run has to equal the total kinetic and potential energy at the bottom of the ski run; energy is conserved, in other words. Now, at the top, there is no there's no kinetic energy and at the bottom, there is no potential energy because the reference level is measured from the bottom. So h will be 0 at the bottom. So we have kinetic energy at the bottom equals the potential energy at the top. And we can solve for v by canceling the m's, multiplying both sides by 2 then taking the square root of both sides and we have v is the square root of 2 g h— square root of 2 times 9.8 meters per second squared times 105 meters, which is, 45.4 meters per second will be the speed at the bottom.
Does anyone know why the 8 degree incline is ignored?
Hi jessicasingh001,
Thanks for the question. Only the change in height is important for questions involving gravitational potential energy, so the 8 degree incline is an extraneous detail. It's the vertical change in height that's important.
Hope that helps,
Mr. Dychko