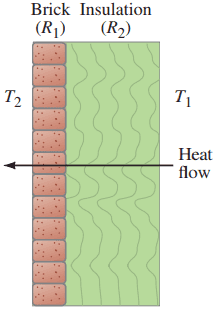
Suppose the insulating qualities of the wall of a house come mainly from a 4.0-in. layer of brick and an R-19 layer of insulation, as shown in Fig.14–19. What is the total rate of heat loss through such a wall, if its total area is $195 \textrm{ ft}^2$ and the temperature difference across it is $35 \textrm{ F} ^\circ$?

VIDEO TRANSCRIPT

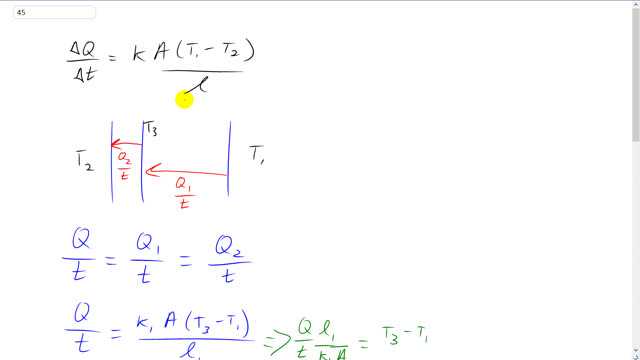
This is Giancoli Answers with Mr. Dychko. The rate of heat conduction across any material is the thermal conductivity of the material times its cross sectional area times the difference in temperatures divided by the thickness of the material. Now, when we have, so, you could say a compound material here where it consists of two different substances touching each other. Then if it's in a steady state where this temperature 1 has been maintained for a long time and this temperature 2 has been maintained for a long time, that means that the rate of heat transfer across the first material equals the rate of heat transfer across the second material, and that equals the total rate of heat transfer across the combination as well. Because if that was not true then it would mean the temperature is changing somewhere in here. But that contradicts the idea that things have been, you know, things have been maintained with these temperatures here for a long time. So, after a while, there's not going to be any temperature changes within the wall. Eventually is gonna reach some steady state where the rate of heat transfer across all the sections are the same. So that is to say that Q over t, the overall rate of heat transfer across the entire wall is equal to Q1 over t, the rate of heat transfer across the first material, and that equals Q2 over t, rate of heat transfer across the second material. So, we'll call the temperature inside the room t1 and outside the room t2, and then this temperature here in between them is going to be t3. And... And so we can write the rate of heat transfer in terms of this first section here which has the insulation. So, that's the thermal conductivity of insulation times its cross sectional area times t3 minus t1 divided by the thickness of this insulation. And we can solve or we can rearrange this to solve for t3 minus t1, and multiply both sides by l1 and divide by k1 A. And you get Q over t times l1 over k1 A is t3 minus t1. And the reason that's useful is because when we express this same Q over t in terms of the brick, we can solve it for the temperature difference and we get t2 minus t3. And then we can add these equations together and we'll end up having the t3's cancel each other. So, this is the thermal conductivity of brick, and it's t2 minus t3 and divided by the thickness of the brick, l2, and when we add the two left sides, we get this. Not much we can do with that, except just rewrite them with an addition between them. And on the right hand side, though, we have t3 minus t1 plus t2 minus t3, and the t3's cancel away because they have opposite signs. Now, recall that that R value is thickness divided by thermal conductivity. So, we can replace this l1 over k1 with R1, the R value of insulation. And then likewise, l2 over k2 can be replaced with the R value of brick. And we can factor out the Q over t, and so that means we have Q over t times R1 over A plus r2 over A is the difference in temperatures t2 minus t1. And solve this for Q over t and by multiplying both sides by A over R1 plus R2. And that cancels on the left, leaving us with Q over t. And on the right hand side we have t2 minus t1 times A over R1 plus R2. And the area is 195 square feet times 35 Fahrenheit degrees, temperature difference, between t1 and t2 inside and outside of the room, divided by 19 is the R value of the insulation. And brick will take to be an R value of 1, it tells us a range of possibilities here for our value of brick. It says it could be anywhere between 0.6 and 1. And that's for 3.5 inch thickness. And we have a 4 inch thickness of brick. So, let's take the upper possibility of 1 for the R value. And that gives about 341.25 or 340 BTUs per hour of heat transfer across the wall.