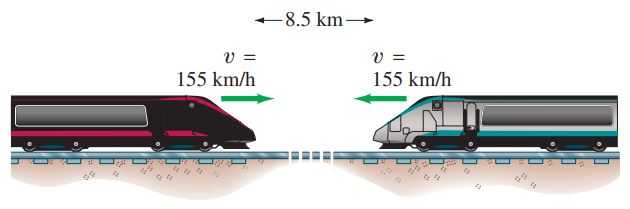
Two locomotives approach each other on parallel tracks. Each has a speed of 155 km/h with respect to the ground. If they are initially 8.5 km apart, how long will it be before they reach each other? (See Fig. 2–35.)
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. These trains are initially separated by 8.5 kilometers; train 1 is traveling to the right at 155 kilometers an hour and train 2 has a velocity to the left of 155 kilometers an hour. We'll take the position of train 1 to be x 1 initial equals 0 and the initial position of train 2— x subscript 2 for train 2 initial is gonna be positive 8.5 meters to the right of sorry that's 8.5 kilometers to the right of train 1 or the initial position 0 and we have to figure out at what time will the separation between these two trains be 0? The separation between them is the position x 2 minus position x 1 and when is that separation 0? So we have expressions for positions for each of the train here; here the position of train 2 is the initial position of train 2 plus the velocity times time this velocity is gonna be negative by the way because it's to the left so this position 2 is gonna be 8.5 kilometers eventually it will be minus some quantity there because velocity's negative. And then the position of train 1 is gonna be its initial position which is just 0 but I wrote it there just to make the formula complete and look better plus its velocity v 1 multiplied by time; both trains are traveling for the same period of time here so we don't need a subscript 2 or 1 on the t there. And so rewriting the separation substituting in for x 2 is x 2 initial plus v 2 t and then minus x 1 which is (x 1 initial plus velocity 1 t) that equals 0 because that's when the trains will meet when the separation between them is 0. So this term here goes bye-bye because that's just 0 we defined the initial position of train 1 to be the 0 point and we are gonna take this term to the right-hand side by subtracting it from both sides gives us a negative x 2 initial and that leaves us with these two terms containing the letter t which we are gonna solve for, this minus sign here goes into the bracket to make this a negative or minus v 1 t and we can factor out the t now and it makes t times velocity 1 minus velocity 2 equals positive x 2 initial; I did a little bit of negative sign trickery there by multiplying everything by negative 1 just to make this term on the right-hand side positive. So it became positive and then the signs of every other term has to change too so now the v 1 is now positive and the v 2 term is now negative. OK And you don't have to do that by the way, you could have a negative 8.5 and then have the other velocities as they are here if you would like. Now we are gonna solve for t by dividing both sides by v 1 minus v 2 and so it cancels on the left and we solve for t then is initial position of train 2 minus the difference in velocities. So that's 8.5 kilometers minus 155 kilometers an hour is the velocity of train 1 and then minus from the formula and then a negative sign because the velocity of train 2 is to the left and we define right as the positive direction. And so that's 155 minus a negative makes a plus there and this results in 0.0274 hours and we'll turn that into units that we can relate to better, say seconds, by multiplying by 3600 seconds per hour giving us 99 seconds before the trains reach each other.
Why S=x2-x1
Why they have the same time
Hi joseotilio25, you're keeping me busy today. :)
First, your question "Why ": is the separation between the trains, is the position of train 2, and is the position of train 1. The distance between the trains is the difference between their positions. Make sure you're not thinking of the "x's" as representing a distance. Only is a distance, whereas each is a position. When you subtract from , you get the distance between these positions. Just to illustrate, if one object is at a position of , and a second object is at a position of , their separation would be .
Your second question "Why they have the same time": We begin looking at both trains at the same time (call it if you like), and we need to figure out at what future time they will meet. Since is the same for both trains, and is also the same since they will both report meeting at the same moment (this isn't chapter 27 on relativity, after all), the elapsed time, which is what represents (perhaps better written as which is ) is the same for both trains.
Why does X2 = X2i + V2 (T)?
Hi swedesanddanes, I'm guessing that the confusing part is the in , correct? For most questions it's typically enough to say something like , but the reason this is usually OK is that normally you choose the initial position to be zero, in which case would be the same as since when the initial position is zero. This question, however, is not one of your usual questions. The second train begins at an initial position of , in which case , so this initial position term is needed in the position formula.
Just to check your understanding, notice how we could have instead chosen after all, but then the initial position of train 1 would need to be (assuming positive is directed toward the right).
Hope this helps,
Mr. Dychko
Hello sir, can't you just cross multiple instead of doing all those steps.
I did 155km/1hr = 4.25km/xhrs
I used 4.25 instead of 8.5 because they are going at constant speed so they both only need to go half of that distance to touch each other.
Did I just get lucky or is this a valid way to solve?
Why do you have .0274 and not .027? Wouldn't the Sig figs go with the lowest and make it .027? (edit) I realized I did mine a different way, disregard.
Find us on:
