A rock is dropped from a sea cliff, and the sound of it striking the ocean is heard 3.4 s later. If the speed of sound is 340 m/s, how high is the cliff?

VIDEO TRANSCRIPT

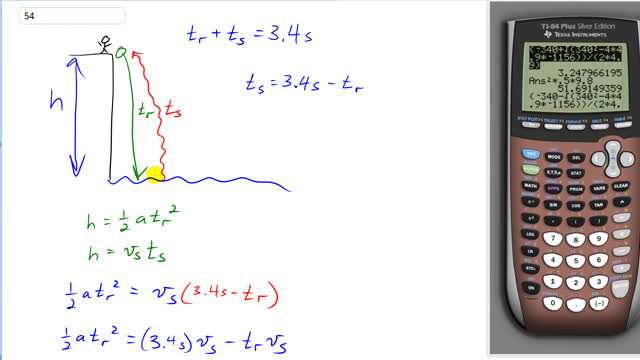
This is Giancoli Answers with Mr. Dychko. So the rock falls from the cliff and it takes some time t subscript r for rock to hit the water as it falls this height h off the cliff. And then after it hits the water, a sound is produced and it takes the sound some time to get back up to the listener or the person who threw the rock up here at the top of the cliff. So the total time between when the rock is dropped and when the sound is heard is this time for the rock to fall plus the time for the sound to get back up the cliff and that total is 3.4 seconds. And we can write expressions for the cliff height in terms of the time that the rock takes to fall and in terms of the time it takes for sound to travel and for the rock falling, it has acceleration and so its height is well v initial times time plus one-half at squared but the initial speed is zero because it's dropped and it's not thrown down so that's why the expression for this height is only one-half at squared. and then when the sound is traveling, it's going at constant speed, you know, gravity is not gonna slow the sound down so its distance traveled is just gonna be its speed multiplied by the time it takes. And we know the speed is 340 meters per second and we can make a substitution for the time that the sound spends traveling using this formula here and we'll subtract the time that the rock travels to get this here. So this time that the sound spends traveling is the total time—3.4 seconds— minus the time that the rock spends falling and we'll substitute that here. And here we have equated the two heights the rock is falling the height of the cliff and the sound is also traveling the same distance h and so we can set this one equal to this one which we have done here and we have also made the substitution in red for time sound by expressing it in terms of the time that the rock spends falling to reduce our number variables. And then we can distribute the v s through the brackets here by multiplying both things by it to get the next line and then we are here. And then this is a quadratic equation and so we are gonna move both things to the left side here so that we have it in the usual form so that we can apply this x equals negative b plus or minus square root b squared minus 4ac all over 2a. quadratic equation formula for this quadratic equation and we are taking down to be positive by the way just to simply our work a little bit; we're not gonna have to worry so much about negative signs. And we have acceleration then is positive 9.8 meters per second squared and times that by half and that's time for the rock to fall squared plus the speed of sound 340 meters per second times time of the rock minus 3.4 multiplied by speed of sound— 340 meters per second. And working through that, we get this that we plug into our calculator and we get 3.24797 seconds for the rock to fall and then using that time, we'll figure out the height using this formula. And when you are doing a reality check on this number, obviously it should be less than 3.4 and 3.2 seems reasonable you know, just like the last because the speed of sound is so much faster than the rock falling, we'd expect rock to take most of the time and almost 3.4 and then for the sound to take a little bit extra to make the total 3.4 seconds. So the height then of the cliff is one-half times its acceleration— 9.8 meters per second squared— and then times by the time the rock spends falling square that and we get 52 meters must be the height of the cliff. And when using that quadratic formula, you could have put a minus sign in there and you would have gotten negative time which on the one hand is doesn't really make much sense and yeah, we'll just leave it at that.