
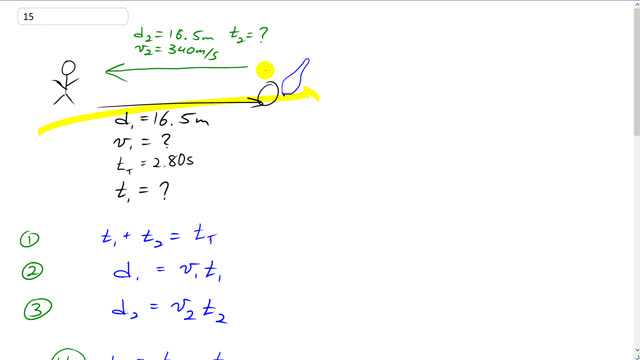
A bowling ball traveling with constants speed hits the pins at the end of a bowling lane 16.5 m long. The bowler hears the sound of the ball hitting the pins 2.80 s after the ball is released from his hands. What is the speed of the ball, assuming the speed of sound is 340 m/s?
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. So this bowler launches the ball along the bowling lane and hits the pin and then after it hits the pin, some sound is produced from that collision and the sound travels back to the bowler and that total time between when the ball was released from his hand and then the sound returns to his ear that total time is 2.8 seconds. Our job is to figure out the speed of this ball and I'll first start by saying how not to answer the question; you cannot take the distance—16.5 meters— and divide it by the time of 2.80 seconds because this 2.80 seconds is not the time that the ball spends traveling; it's the time that the ball spends traveling plus it also includes the time for the sound to go from the pin to the bowler. Now admittedly, you will get fairly close by using this calculation because the sound travels really fast and so that's going to be a very small amount of time but nevertheless, if you want to be precise to anymore than two significant figures, you should not do this and if there's a large distance here then the time that the sound spends traveling would be more significant. OK. So what we are gonna do is first, you know, do some book-keeping and just keep track of all the variables involved; the distance traveled by the ball, d 1 is 16.5 meters, and it's going at some unknown speed that we have to calculate. The total time for this round trip of the ball leaving his hand and then the sound returning to his ear is 2.8 seconds and the trip of the sound it's going the same distance 16.5 meters and is traveling at a speed of 340 meters per second and we don't know what t 2 is either all we know is what t 1 plus t 2 is and it's the total time and we'll call that equation 1. Equation 2 will express the distance of d 1 in terms of v 1 and t 1 and then d 2—same idea—speed of sound plus t 2 that we don't know. And we now have a system of equations a bunch of equations containing the same variable and we can substitute from one into the other until we solve for the thing we want to find and we know it's possible when we have number of variables is equal to the number of equations. So we have t 1, that's one variable; we have t 2, that's another variable and d 1 is another variable or sorry d 1's not really a variable because we know it and d 2's the same we don't know v 1, that's the other variable there we go. So we have three variables and we have three equations so that means we can go off to the races, we can solve this. If we had four variables, we would have to find a fourth equation. OK. So we are gonna rewrite equation 1 as version b and we are gonna bring this t 2 to the right-hand side by subtracting it from both sides giving us t 1 is t total minus t 2. And then we'll substitute that into equation 2 so we are rewriting equation 2 here and labeling it 2 version b that's d 1 is v 1 times instead of t 1, we are gonna write t total minus t 2 and then we'll switch equation 3 into this form; we'll solve it for t 2 because we are gonna substitute in for t 2 here in a moment so equation 3 is d 2 divided by v 2 when you divide both sides by v 2 here and then we'll substitute equation 3 version b into equation 2 version b so we are just going like this, in other words, and t 2 is gonna get replaced by d 2 over v 2 and t total copied, v 1 copied, d 1 copied and here's equation 2 version c which we can solve for v 1 which is the whole question— what is the speed of the bowling ball, v 1? We'll divide both sides by this bracket t total minus d 2 over v 2 and the same with the left-hand side and then switch the sides around so you have the unknown v 1 on the left and it's gonna be 16.5 meters divided by 2.80 seconds minus 16.5 divided by 340 meters per second giving us 6.00 meters per second is the speed of the bowling ball.
For d2, why is the value not -16.5 m, since the direction is from the pin back to the bowler?
Hi aheumangutam, thank you for your question. There are two ways to look at it:
- Be strict with negative signs. This is what your comment is suggesting, and it's totally a fine approach of course. Sometimes it's the best approach. Being strict with negative signs would also require making velocity of the sound when it returns from the pin negative. In this case the negative displacement of sound returning from the pin would divide by the negative velocity in , resulting in the same positive answer for .
- Treat as a distance. This is how I was thinking about it in the video. There's no advantage to being strict with negative signs in this particular problem. I suppose it takes a bit of problem solving practice to know when it acceptable to ignore negatives. It's OK to do it here since the displacement of each leg equals the distance of that leg... if in doubt though, go with your option 1 by being strict with negatives.
All the best with your studies,
Mr. Dychko
I dont understand what you did in this video can you please explain it?
Hi rafih6, I'll give it a try, but if this doesn't help then try again with a more specific question. The general idea in this question is that you know the total time for two different things to finish travelling the same distance. The distance is the separation between the bowler and the pin. The first thing travelling is the ball towards the pin, and the second thing travelling is the sound of the impact which takes some time to travel from the point of contact with the pin back to the bowler. I set up three equations to summarize these points, then do some algebra by doing substitution between equations to combine them and eliminate unknowns.
Maybe that helps?
Mr. Dychko
Well, if the person's ear is 1.7 meters on average above where he threw the ball, and the speed of sound goes in radius, then you could use the pythagoreas theorem to check the most accurate distance between where the ball hit and the person's ear, and use that instead of just the distance of the bowling lane.