
A rocket rises vertically, from rest, with an acceleration of until it runs out of fuel at an altitude of 775 m. After this point, its acceleration is that of gravity, downward.
- What is the velocity of the rocket when it runs out of fuel?
- How long does it take to reach this point?
- What maximum altitude does the rocket reach?
- How much time (total) does it take to reach maximum altitude?
- With what velocity does it strike the Earth?
- How long (total) is it in the air?
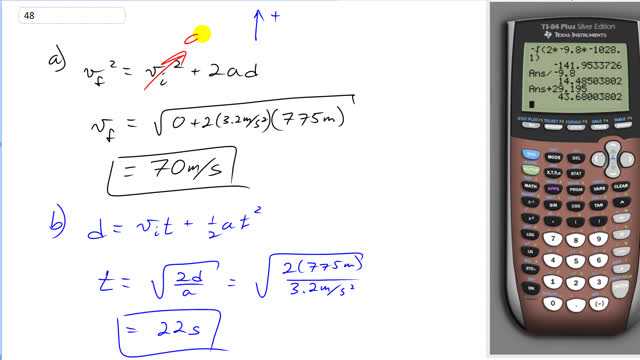
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We'll take upward to be positive and this is the final velocity of the rocket squared when it runs out of fuel equals its initial velocity which is zero we are told—it starts from rest— plus 2 times acceleration times the height that it reaches. So the final velocity then will be the square root take the square root of both sides here square root of all this and we are taking the positive square root because we know it's gonna be directed upwards 0 is the initial velocity plus 2 times its acceleration—3.2 meters per second squared— times the height that it reaches— 775 meters— for a final velocity of 70 meters per second and then I'll show you in the calculator what the unrounded answer is just so you see that too— it's way up here, holy smokes long question— okay. So two significant figures in our acceleration so two significant figures in our answer for the velocity 70 meters per second upwards is the velocity when it runs out of fuel. How long does it take to reach that point? Well, here's the height that's given and we know the initial velocity is zero so that term disappears and we'll do some algebra here to solve for t. So times by 2 and divide by a and then take the square root of both sides and you get t equals square root 2 times the height divided by acceleration. So square root of 2 times 775 meters divided by 3.2 meters per second squared that gives 22 seconds to reach that height where it runs out of fuel. Now, even though it runs out of fuel, it's still gonna be going upwards and the question is what maximum altitude will it reach? So here's the h 1 is this height that it reaches when it runs out of fuel so that settles up to that point and then it's still gonna go some distance further upwards; it has an acceleration that's downwards but it's still gonna have a velocity upwards until the point where it gets to this maximum height when the velocity is zero at which it point it will turn around and start to fall back to the ground. So since we know that that's zero, this formula is useful because v f is zero and initial velocity we found in part (a) already and see that v i is the v i here— when it runs out of fuel— that's the v i we are concerned with in this formula, in this context. So d is h 2 in my drawing here so I have replaced letter d with letter h 2 here; h 2 is the negative of v i squared divided by 2a so I took this v i squared to the left side and then divided both sides by 2a and you are left with this plus the negative of the initial velocity here when it runs out of fuel of 70.427 meters per second and square that divide it by 2 times the acceleration downwards of 9.8 so that's negative 9.8 meters per second squared and that's the second portion of it rise that's 253 meters and we'll add that to the initial amount of height it reaches— 775 meters— to get a total height of above the ground of 1030 meters and that's all the way down to here in the calculator and then we'll scroll some more space here. And then next question is how much time does it take to reach the maximum altitude and that consists of two different portions of time; the first portion of time we have already calculated as our answer to part (b) that's the height to the point where it runs out of fuel so that's 22 seconds and then we have to add to that this portion of time that it takes to travel to this second height h 2. Now at the very top, the velocity is gonna be zero that's at the very top here we use the same trick in this part (c) and the initial velocity is likewise for part (c), this point here where it runs out of fuel and we are solving this for t 2 and subtract v i 2 from both sides and then divide by a and you get negative 71.427 meters per second divided by negative 9.8 meters per second squared for this time of 7.186 seconds and we add that to the 22 seconds it takes to get to the point where it runs out of fuel for a total of 29 seconds to get to the very maximum height. With what velocity does it strike the ground? Well, we know that it starts with a velocity of zero; now what can be confusing throughout this solution is that I'm using the letter v i to represent initial speeds at different times and so this is the same letter v i but it means different things for each different part of the question. I could have used a whole bunch of other different subscripts but I think that would be even more confusing so I'm just explaining it each time. So v i is the velocity at the very top before it starts to fall and then it falls this 1030 meters and the only acceleration involved here is that due to gravity so it's negative 9.8 meters per second squared and it is just a regular, you know, 'body from rest falls a certain distance' this type of question and we are gonna solve for the velocity down here when it hits the ground. So the final velocity we'll take the square root of both sides here and after we get rid of this v i business because it's zero and we are gonna take the negative square root because we know it's directed downwards and I mean it could be plus or minus but we'll take the minus in this context. So square root of 2 times negative 9.8 meters per second squared times sometimes I get questions from students, you know, to do with negative signs within square roots and then the calculator complains not a real answer and so on so I'm explaining why this d is a negative number because d is always supposed to be displacement; this is meant to be a vector not a distance not a scalar. So as a vector or as displacement, in other words, it should be the final position minus the initial position so that's y final minus y initial or call it what you will, d final minus d initial. And so the final position is zero minus the initial position of a 1030 meters or a 1028.1 meters up so this 0 minus this positive number becomes ends up being a negative times this negative makes a positive and so you can take the square root of it without your calculator complaining. and we get a final velocity of 140 meters per second; that is two significant figures in that answer so that's why I round it to 140 because there's two significant figures in this— well, I guess there's three maybe, I don't know. I don't really wanna have a significant figures argument but I guess your teachers might get on your case about it so let's make that 142 meters per second because I guess this 1030 meters has three significant figures in it. OK. Now the total time in the air is the last question and we have the total time that it takes to get to the maximum height which we have already calculated in part (d) so that's 29 seconds plus the time it takes to fall from the maximum height. So define t 3—the time it takes to fall from the height of 1030 meters— we use this formula and v f we know now because we just calculated it in part (e) and we'll divide that velocity by the acceleration and v i is zero because that's the time it takes to fall from this maximum height where v i is zero and we are dividing both sides by a to solve for t 3 and we are flipping the sides of the equation around so t 3 is on the left and we get 14.485 seconds add that to the time that he takes to get to the top for a total time of flight of 44 seconds.