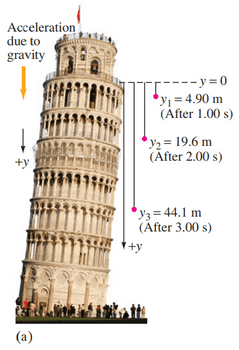
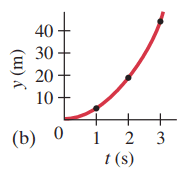
For an object falling freely from the rest, show that the distance traveled during each successive second increases in the ratio of successive odd integers (1, 3, 5, etc.). (This was first shown by Galileo.) See Figs. 2-19 and 2-22.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. We'll take downward to be the positive direction and so the position will be one-half at squared; it has no initial downward velocity and no initial position we'll take its starting point to be position zero and so we don't need this whole convoluted version here all those other first two terms are zero and a is 9.8 meters per second squared so one-half of that is 4.9 so our position at any particular time n seconds is 4.9 times the time squared. Now to find the ratio of the distance traveled during a particular second as a ratio of the distance traveled during the first second is this expression so the distance traveled in the nth second minus the distance traveled in the second just previous to it as a fraction of the initial distance that's actually what we are trying to show is a series of consecutive odd integers so we'll substitute into each thing here. So the distance traveled in a second just prior is 4.9 times the amount of time just prior squared and the amount of time was 1 second previous to the current time t n so we have t n minus 1 and so substituting that in for this we get that the distance traveled the second before and the nth second minus 1 so that's a second before the nth second is 4.9 times t n minus 1 all squared and so that means we are working on the numerator here this fraction so we have the distance traveled in the nth second minus the distance traveled in the second before that is 4.9 times t n squared is substituting for this distance and then minus 4.9 times t n minus 1 squared which is substituting for the distance of the second just prior and then we'll expand this bracket to get this here. So t n minus 1 squared is t n squared minus 2 times t n plus 1 and then we'll distribute the 4.9 into the bracket multiply each term by 4.9 and we get 4.9 t n squared and then oh it's a minus there so it becomes positive 9.8 t n and negative 4.9 and these two terms are the same with opposite signs so they make zero and we have 9.8 minus 4.9 and instead of calling it 9.8, we can call it 2 times 4.9 just because that's gonna make things look a little nicer as you'll see in a second. We can substitute all of this into the numerator of this fraction and that's rewritten here; since I have written it 2 times 4.9 instead of writing it 9.8, we can say that 4.9 is a common factor; yeah by the way, d 1 is the distance traveled during the first second so that's just 4.9 times 1 you know, squared if you like, you know to be absolutely rigorous and correct but you know, 1 squared is just 1 so we have 4.9 on the bottom there; it's a common factor so it cancels into both terms on the top and we have 2 times t n minus 1 is the result of this fraction. And this is a sequence of odd integers because t n is 1 second and then it's 2 seconds and then it's 3 seconds and so we substitute in 1, 2 and 3 into this formula, 1, 2 and 3 and we get then the answer 2 times 1 minus 1 is 1 and then we get 2 times 2 is 4 minus 1 is 3 2 times 3 is 6 minus 1 is 5 so 1, 3, 5 we are showing that this distance traveled during each second is an odd integer times by the distance traveled during the first second.