
A driver is traveling 18 m/s when she sees a red light ahead. Her car is capable of decelerating at a rate of . If it takes her 0.350 s to get the brakes on and she is 20.0 m from the intersection when she sees the light, will she be able to stop in time? How far from the beginning of the intersection will she be, and in what direction?
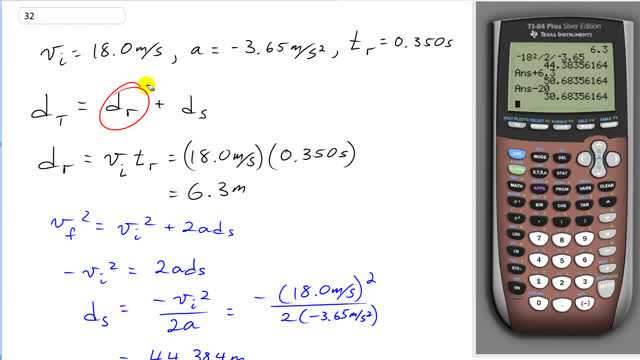
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. The total distance this driver will travel will be the distance she travels while reacting to the red light this is before she presses the brakes on and during which there is no deceleration and then add to that the distance that she travels while the brakes are being applied. So the distance traveled during the reaction time is the initial speed times the reaction time so that's 18 meters per second times 0.350 seconds and that gives 6.3 meters and then to figure out the distance traveled while stopping, we use this formula which has all the things known except for the distance while pressing the brakes, while stopping final speed is zero we'll subtract v i squared from both sides and we get negative v i squared equals 2ad s for stopping and then divide both sides by 2a and then switch the sides around and we get d s equals negative v i squared over 2a. So that's negative of 18 meters per second squared divided by 2 times the acceleration of negative 3.65 meters per second squared. So that's 44.384 meters traveled while the brakes are being depressed for a total of 50.68 meters distance traveled from the time the red light begins and she has this reaction time distance of 6.3 meters before the brakes are applied plus this. So that's way more than 20 meters away from the intersection and so she'll definitely not stop in time and she'll be 30.7 meters past the intersection by the time she comes to a stop.