
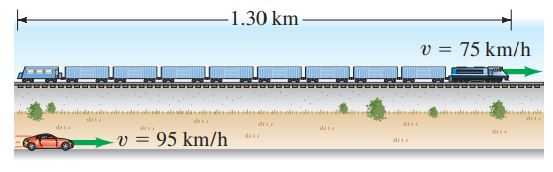
An automobile traveling 95 km/h overtakes a 1.30-km-long train traveling in the same direction on a track parallel to the road. If the train's speed is 75 km/h, how long does it take the car to pass it, and how far will the car have traveled in this time? See Fig. 2–36. What are the results if the car and train are traveling in opposite directions?
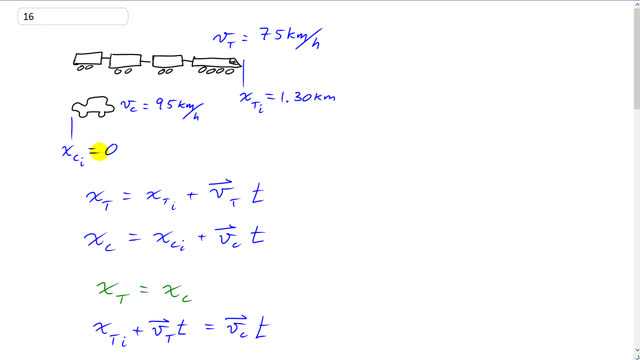
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This train is traveling to the right at 75 kilometers an hour and this car is traveling to the right at 95 kilometers an hour. We'll take the car's initial position to be zero and the train's initial position is 1.3 kilometers to the right because that's how long the train is. So we are gonna figure out at what time is the car's position the same as the train's position and we have expression's for each of the position's here; the position of the train is the train's initial position plus its velocity times time and then the position of the car is its initial position plus velocity of the car times time well the car's initial position is zero so this term disappears. And x T equals x C; that's the moment when the rear of the car is at the nose of the train and keep in mind that these x's don't represent distances rather they represent positions and we'll calculate distances in a moment. So the position of the train is we'll just copy it here x T initial plus velocity of the train times time equals velocity of the car times time substituting in here. And then we'll bring this term to the right-hand side by subtracting it from both sides but then we'll flip the equations around the sides around so that we have the unknown, t, on the left. So we bring this to the right-hand side which makes it a minus v T times time and then flip the sides of the equation around and then we have v Ct minus v Tt equals position of the train initially. And we'll factor out this common factor time here and we have time multiplied by velocity of the car minus velocity of the train equals position of the train initially and then divide both sides by this bracket and we get that the time it takes for the car to reach the nose of the train is gonna be the train's initial position divided by the differences in their velocities. So we have 1.3 kilometers divided by 95 kilometers an hour— velocity of the car— minus 75 kilometers an hour— velocity of the train— and that gives 0.65 hours which we'll multiply by 60 minutes per hour to turn it into minutes which is 3.9 minutes. And the distance the car travels is gonna be the car's velocity times time and so that's 95 kilometers an hour times 0.065 hours which is 6.2 kilometers. I guess I should have said speed rather than velocity but anyway, they are the same in this case. So in part (b), what if the train is moving towards the car? Well, in that case, wonder if I can do something fancy here say flip horizontal, look at that nice. So now we have the train going the other way and the train's initial position is still here because this is, you know, it's at the rear of the train now but it's in the same place it's 1.3 kilometers away from where the car is initially and the question is still the same; when is the rear of the car gonna meet the end of the train that happens to be this end now. And so we have the train going to the left now and its velocity will be negative everything, algebraically speaking, is exactly the same except that the velocity's now negative 75 kilometers per hour and that means this bottom of this fraction is gonna be a bigger number because now it's in fact going to be a plus at the bottom there and so that's gonna make the quotient or the result of this division smaller because we are not dividing by a bigger number and we get 0.007647 hours times 3600 seconds per hour and that gives 28 seconds is the amount of time for the car to overtake the train when they are moving towards each other and the distance the car would travel in that time is 0.73 kilometers.
Thank this page is amazing. I love it. I'm improving a lot thank for such a beautiful job.
Thank you joseotilio25 for such nice feedback! I'm really glad the solutions are helping.
Best wishes with your studies,
Mr. Dychko