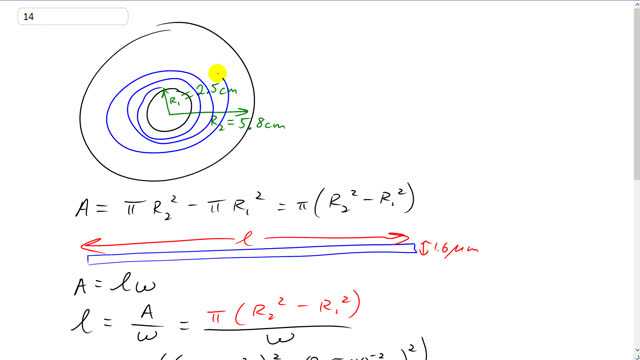
Digital bits on a 12.0-cm diameter audio CD are encoded along an outward spiraling path that starts at radius $R_1 = 2.5 \textrm{ cm}$ and finishes at radius $R_2 = 5.8 \textrm{ cm}$. The distance between the centers of neighboring spiral-windings is $1.6 \; \mu \textrm{m} \; (= 1.6 \times 10^{-6} \textrm{ m})$.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. So the spiral path that the laser reads along on the CD starts at about 2.5 centimeters and spirals out till it gets to the outer radius of the CD of 5.8 centimeters and our first question is what length would the spiral path have? and we are given a tip in the problem that says imagine you were to unwind it into a rectangular straight path this rectangle would have the same area as the total area here. So the area's gonna be the area of the full circle so that's this whole thing including the center that's πR 2 squared and then subtract the area of this hole in the middle so that's πR 1 squared and that's gonna be the area over which the spiral path exists. And we unravel it and it has some length that we have to find and it has a width of 1.6 micrometers we are told and so the area of this rectangle is length times width and we'll solve for l by dividing both sides by w and then switch the sides around so we have the unknown l on the left. So the l is the area divided by the width of the spiral path and so the area is π times R 2 squared minus R 1 squared and that's divided by w. So we have π times 5.8 times 10 to the negative 2 meters that's 5.8 centimeters expressed in meters so centa is the prefix meaning times 10 to the minus 2 and so we'll substite in our you know, mks units—meters, kilograms, seconds—is typically what we change units into so that everything works out nicely in our formulas and we have minus 2.5 times 10 to the minus 2 meters squared all divided by the 1.6 times 10 to the minus 6 meters. So 10 to the minus 6 is what you put in place of the prefix micro so you know work that out and it makes about 5400 meters about 5.4 kilometers is the total length of the spiral path that the laser travels over on the CD. And the time it takes to travel that path is gonna be the length of the path divided by the speed. So it goes 5378 meters divided by 1.2 meters per second and we get this answer in seconds and we'll convert that into minutes say so we have a unit that we can relate to a bit better. So we'll times by 1 minute for every 60 seconds and this gives us about 75 minutes total playtime you would expect on a CD.