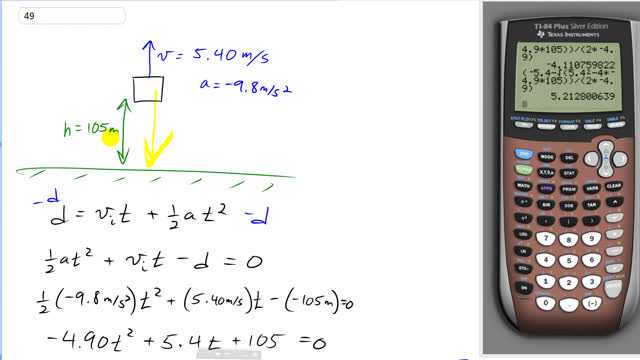
A helicopter is ascending vertically with a speed of 5.40 m/s. At a height of 105 m above the Earth, a package is dropped from the helicopter. How much time does it take for the package to reach the ground? [Hint: What is $v_0$ for the package?]

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. The helicopter is moving upwards with a speed of 5.4 meters per second and when it finally reaches this height of 105 meters above the ground that's when it releases the package and so at that point—this is the picture— the package is going up with 5.40 meters per second with an acceleration downwards of 9.8 meters per second squared and so we have the negative to reflect the direction downwards for the acceleration. And we have the height of the package is given by its initial velocity times time plus one-half acceleration times time squared and we are going to solve for t by subtracting d from both sides and then put everything on the left side and then substitute for all the numbers. The thing to be cautious with in this question, in this algebra is to substitute the correct signs, the negatives and positives. So the acceleration is negative downwards I guess we should state our coordinate system here upwards is positive acceleration is negative 9.8 meters per second squared let's multiply it by half or negative 4.9 here the velocity is initially upwards of 5.4 meters per second so that's positive 5.4 and then we have a minus sign from our algebra from subtracting d from both sides and the displacement is also negative because displacement is the final position minus the initial position so the final position is zero if we define ground to be the zero point minus the initial positive height of a 105 so this displacement or this Δd becomes negative 105 as a result of this minus sign here. So that's minus negative 105. So we have all these things are getting substituted into the quadratic formula And we have negative 5.4 is negative b and then plus or minus the square root of 5.4 squared minus 4 times a which is negative 4.9 and then times c which is positive 105; these two minuses make a positive here and then that's divided by 2 times a. Now we take the positive result because that's the only one that really makes sense first of all and secondly, there is an interpretation for this negative 4.11 answer. So we got the positive result for time by having a minus sign in the numerator here; this negative time interpretation, by the way, is for the case where the package was in it supposes that this equation here is true for all time which it isn't because the package is initially on a helicopter in which case, it has no acceleration downwards at all it has only a velocity upwards of 5.4 when it's in the helicopter but the equation doesn't know that, the equation just thinks that the package has a vertical position defined by this equation and it says well, if the package was initially launched from the ground such that it has a speed of 5.4 upwards at this height, this position would have been at the ground 4.11 seconds prior to being here; just if you are curious to know to understand what that means that negative. or when you look at it here, 4.11 seconds ago is when it would have been at the height zero. OK. So 5.21 seconds is when the package will reach the ground.