A runner hopes to complete the 10,000-m run in less than 30.0 min. After running at constant speed for exactly 27.0 min, there are still 1200 m to go. The runner must then accelerate at $0.20 \textrm{ m/s}^2$ for how many seconds in order to achieve the desired time?

VIDEO TRANSCRIPT

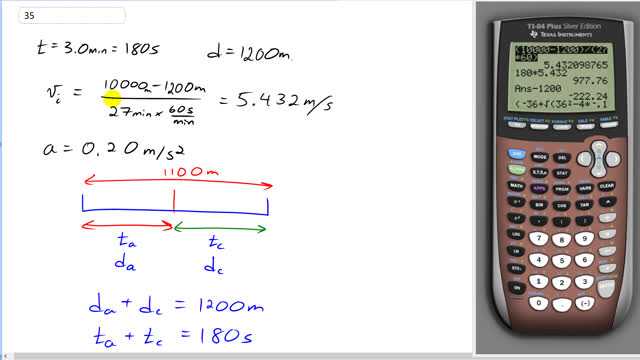
This is Giancoli Answers with Mr. Dychko. This runner has 3 minutes or 180 seconds left in the race and 1200 meters to cover. Their initial speed is the 10000 meter total distance minus the 1200 meters still to go divided by the 27 minutes converted into seconds that they have taken to run that distance and so that constant speed they have been traveling so far is 5.432 meters per second. And so this is going to be their acceleration 0.20 meters per second squared. Now the thing to consider is that they are going to accelerate for some period of time over this 1200 meters and then they will finally reach some final speed at which they will be at constant speed for the remainder of the 1200 meters and we don't know how this is gonna be divided up; whether they are gonna accelerate for most of it or only part of it and we have to figure out what that time will be. What we do know is that the distance traveled during acceleration plus the distance traveled at constant speed is a total of 1200 meters remaining and we know that the time that they spent accelerating plus the time that they spent at constant speed is the total 3 minutes left in the race—180 seconds. And we can come up with other expressions for this distance; the distance while accelerating is gonna be this expression their initial speed—which we have already calculated—times the time that they spend accelerating— which we don't know— plus one-half at squared. And then add to that the distance traveled at constant speed which will be the final speed at the end of this acceleration— that's the speed that will be at here— times the amount of time that they spend at constant speed which we also don't know. But we can substitute for both of these things in terms of t a and then we'll have a formula containing only one variable that's unknown which is the time spent accelerating and that's what we have to solve for in this question. So we have the final speed at the end of this interval of acceleration is gonna be the initial speed which is happening here plus the acceleration that is also known times this unknown t a. And then the time spent at constant speed will be 180 minus whatever time is spent accelerating and then expanding this bracket out, we get v initial times 180 minus v initial times t accelerating plus 180 times at a and then minus at a squared and these two things are the same with opposite signs so they cancel so let's get rid of those and collect some other terms there and bring the 1200 meters total distance traveled the total distance traveled is 1200 meters to the left-hand side by subtracting 1200 from both sides and then this term combines with this term to make a total of negative one-half at a squared and then we have plus 180at a and then plus 180v i minus 1200 meters and substituting in some numbers here, we have 0.2 meters per second squared is the acceleration and then it's 180 times 0.2 and 180 times its initial speed that we already calculated which happens here and then minus the 1200 meters and we get this here which is a quadratic equation and plugging it into the calculator here using this formula here the solution to this quadratic equation is negative coefficient b which is 36 and plus or minus the square root of b squared minus 4 times the coefficient of the leading term which is negative 0.1, that's a and then times the coefficient of the constant term which is negative 222.24 here and then divide by 2 times a and we get 6.3 is our answer; an alternative solution to this equation is with a minus sign there and that gives 353 but we that's an extraneous solution, we reject it because 353 is longer than the total time remaining so it's nonsensical, it's more than 180. So 6.3 seconds is the amount of time they need to spend accelerating to meet their goal of 30 minutes for 10000 meters.