
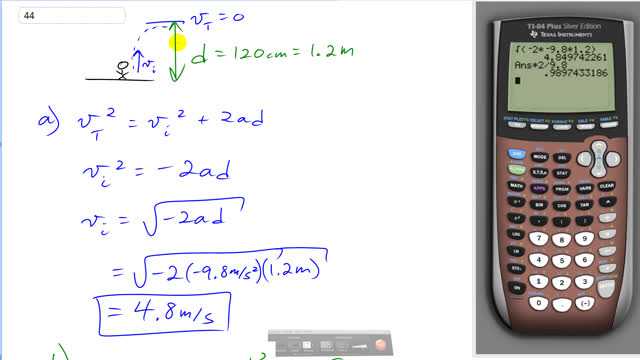
The best rebounders in basketball have a vertical leap (that is, the vertical movement of a fixed point on their body) of about 120 cm.
- What is their initial “launch” speed off the ground?
- How long are they in the air?
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This basketball rebounder leaps up and goes a height of 1.2 meters and at the top of their parabola or at the top of their arc they are jumping their speed is gonna be zero and we can use this formula to figure out what the initial launch speed must have been to reach this height of 1.2 meters. So we can get rid of this term because the speed at the top is zero and then minus 2ad from both sides that gives us the initial velocity squared equals negative 2ad and then take the square root of both sides and we get the initial launch speed is square root of negative 2 times acceleration times the height. So that's square root of negative 2 times negative 9.8 meters per second squared because we are taking upwards to be positive and the acceleration is down so it's negative times a height of 1.2 meters which is 4.8 meters per second upwards. The total time that they spend in the air can be given by this formula; this is the displacement formula and it equals zero because they return back to the starting point and we can divide both sides by t then 0 divided by t is 0 and on the left side, a t cancels from both terms and then we'll subtract the initial from both sides and giving us this line and then we'll multiply by 2 over a on both sides giving us that the total time in the air is negative 2 times the initial launch speed or velocity divided by acceleration. So that's negative 2 times 4.8497 meters per second divided by negative 9.8 meters per second squared which is a total time in the air of 0.99 seconds. Now basketball players actually appear to stay in the air longer than this and I think the reason is that they bend their legs so that they return to a height that's actually lower than what they launched from.
Why don't use d=1.2 in the part B. Because I have d= 1.2 m
Hi joseotilio25, thanks for the question. Quick answer: is displacement, which is zero after the basket ball player lands. Longer answer: It's true that the basketball player jumps in the air, and this figure is used in part a) to find their initial launch speed. Now that the initial speed is known, I chose a method in part b) which uses . This is convenient since the displacement is zero because the basketball player returns to the same position as they started (on the ground). The displacement equation becomes and the video shows the steps to solve for , the total time spent in the air during a jump.
Hope this helps,
Mr. Dychko