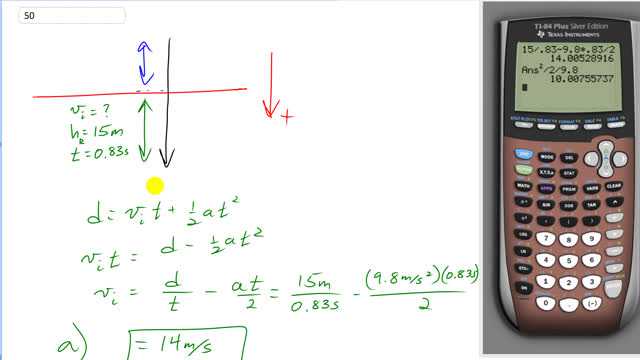
Roger sees water balloons fall past his window. He notices that each balloon strikes the sidewalk 0.83 s after passing his window. Roger’s room is on the third floor, 15 m above the sidewalk.

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. We'll take down to be the positive direction in this question and we have water balloons falling past Roger's window which is at this level on the third floor 15 meters above the ground and then hitting the ground 0.83 seconds later. So the question is with speed are they passing Roger's window what is the initial speed? So we have the displacement is gonna be the initial speed times time plus one-half at squared and rearrange this to solve for v i and we'll subtract one-half at squared from both sides and then switch the sides of the equation around so that we have the unknown v i on the left and then divide both sides by t. So I have chosen to divide each particular term by t here and that works fine. So we have d over t minus a and then just t one of the t's cancel so it's not t squared anymore over a 2. So that's 15 meters divided by 0.83 seconds minus that's positive 9.8 meters per second squared because we chose down to be the positive direction and for the same reason this displacement is also positive because we chose down to be positive and times 0.83 seconds there divided by 2 giving us 14 meters per second must have been the speed the balloon passed Roger's window. Then the next question is from what height did the balloon originally get dropped assuming it was dropped from rest at some height above Roger's window. Well, we'll consider just this interval of height there and at the end of this interval, we'll have some final speed at the end of this drop which is the initial speed of part (a) and the initial speed for this upper portion is zero we are told that the balloon is dropped from rest at some point up here and so we can use this formula relating final and initial speed with the distance and acceleration that you know. So we'll solve this for d by subtracting v i from both sides and then dividing by 2a. And we have this unknown distance above Roger's window it's not the distance above the ground by the way, it's just the distance above the window because we are only dealing with this interval here and that's gonna be 14.005 meters per second and we'll square that that's the final speed of that interval there minus 0 divided by 2 times the acceleration and that gives 10 meters. So 10 meters plus the 15 meters that Roger's window is above the ground because of the total height of 25 meters to the point where the balloon was originally dropped. And there's 5 meters per floor or you can say, 3 floors for every 15 meters because Roger's room is on the third floor and it's 15 meters above so 3 divided by 15 times 25 meters total height meters cancel giving us the number of floors the 5th floor, that's where the balloon was originally dropped from.