A baseball is hit almost straight up into the air with a speed of 25 m/s. Estimate a) how high it goes, b) how long it is in the air. c) What factors make this an estimate?

a) 32 m b) 5.1 s c) d) The biggest estimate here is one that is common for many problems: air friction is ignored. Often air friction is very significant, but we still ignore it since it's quite difficult to account for. Consider that highly skilled engineers still spend enormous amounts of money and time on creating wind tunnels to test the aerodynamics of their designs. They do this because it isn't realistically possible to reliably make calculations to account for air friction, so it's necessary to actually run tests in a wind tunnel. e) The problem doesn't explicitly say the ball returns to the exact same height from which it was hit, but we assumed so in our solution.

Problem 42

A baseball is hit almost straight up into the air with a speed of 25 m/s. Estimate

how high it goes,
how long it is in the air.
What factors make this an estimate?

$32\textrm{ m}$
$5.1\textrm{ s}$
1. The biggest estimate here is one that is common for many problems: air friction is ignored. Often air friction is very significant, but we still ignore it since it's quite difficult to account for. Consider that highly skilled engineers still spend enormous amounts of money and time on creating wind tunnels to test the aerodynamics of their designs. They do this because it isn't realistically possible to reliably make calculations to account for air friction, so it's necessary to actually run tests in a wind tunnel.
2. The problem doesn't explicitly say the ball returns to the exact same height from which it was hit, but we assumed so in our solution.

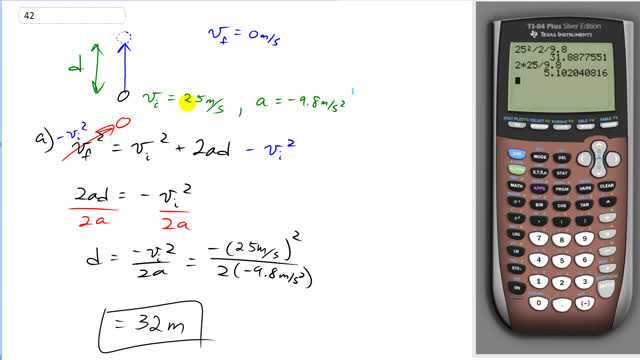
Giancoli 7th Edition, Chapter 2, Problem 42 solution video poster

In order to watch this solution you need to have a subscription.

Get Started

View sample solution

VIDEO TRANSCRIPT

This is Giancoli Answers with Mr. Dychko. When a ball is launched upwards, at its maximum height, it will have a final speed of zero. We are told that it launches with an initial speed of 25 meters per second and we'll take up to be the positive direction in which case its acceleration is negative 9.8 meters per second since acceleration is downwards. We'll start with this formula in order to calculate the maximum height that it reaches; we know the final velocity is zero and so we just subtract initial velocity squared from both sides that gives us 2ad equals negative v i squared then divide both sides by 2a giving us the maximum height is negative initial velocity squared divided by 2a. So that's negative of 25 meters per second squared and then divide by 2 times negative 9.8 meters per second squared and that gives a maximum height of 32 meters. And then in part (b), d means something different now; it's now a zero because the displacement of the ball is zero since it returns back to its initial position. So we are gonna use this formula now to solve for the total time it spends in the air and we can divide both sides by t that cancels the t from both of these terms leaving us with this line here and then subtract v i from both sides so minus v i gets rid of that on the left side and then minus v i on the right side gives us this line one-half at equals negative v i and then times 2 over a gives the time that it spends in the air is negative 2 times initial speed divided by a. So that's negative 2 times 25 meters per second divided by 9.8 meters per second squared is a result of 5.1 seconds in the air.

COMMENTS

By sheumangutman on Sat, 9/24/2016 - 5:44 PM

For the 2nd part of the question, why can't you use the formula Vf=Vo+2at?

Thanks.

By Mr. Dychko on Sat, 9/24/2016 - 6:37 PM

Hi sheumangutman,

Thanks for the question. I think you mean to suggest $v_f = v_o + at$ , correct? That approach would be equally fine, provided you establish that $v_f = -v_o$ , which is true since it returns back to the original launch height. This means your suggested formula, with a substitution for $v_f$ , would become $-v_o = v_o + at$ which rearranges to $t = \dfrac{-2v_o}{a}$ which is the same formula shown at 1:20 in the video. You have to be a little cautious with your suggested formula, however, since it works only when you can tell how the final velocity compares with the initial velocity. $v_f = -v_o$ only when something returns to it's original height. If something fell into a hole after being launched upwards, meaning it returns to a different height, you would be better off using the $d=v_ot + \dfrac{1}{2}at^2$ formula. For this problem, however, the formula you suggest would be just fine.

All the best,
Mr. Dychko

By lcbishop on Sat, 9/24/2016 - 7:13 PM

For part c) What specific factors make this an estimate?

By Mr. Dychko on Sun, 9/25/2016 - 7:25 PM

Hi Icbishop, did you post this question on the wrong video? I don't see a part c) for this problem.

Cheers,
Mr. Dychko

By lcbishop on Sun, 9/25/2016 - 9:00 PM

Well I double checked and I do indeed have a part c on #42 chapter 2. It is the 7th Edition as well. The question also matches up with the solution provided.

By Mr. Dychko on Mon, 9/26/2016 - 6:54 PM

Ah, right you are Icbishop. Sorry about that, I just checked the video without looking at the textbook. I've added some notes to the quick answer above the video.

Cheers,
Mr. Dychko

By idan on Sun, 2/26/2017 - 10:42 PM

By dividing by "t" instead of factoring aren't we losing a physically meaningful answer t=0 (the time the ball was hit)?

By Mr. Dychko on Mon, 2/27/2017 - 8:40 AM

Hi idan, you are making a valid point. You have a sharp eye! Mathematically, it would be more correct to factor and then find the roots of the resulting equation, thereby discovering the answer $t=0$ . However, since this question is asking for the "time in the air", $t=0$ , as you know, is an extraneous solution, so the effort of finding the solution $t=0$ and then discarding it as extraneous isn't worth the effort. The technique in the video is perfectly fine for a physics class, since math is just a tool for finding solutions to the physical problem, which in this case is "how much time is the ball in the air", not "at what times is the ball at height zero". For the latter, one must follow the technique you suggest by factoring since $t=0$ would be a non-trivial solution, but as it is, $t=0$ is not a solution for determining the "time in the air" problem. In a math class there's no question that to answer "solve this equation", one must factor and include $t=0$ as a solution.

All the best,
Mr. Dychko

By EddieG on Thu, 9/6/2018 - 1:50 AM

Question #39 a ball is thrown straight up with a speed of 36 m/s. how long does it take to return to its starting point. Question is my teacher teaches out of 7th edition I have 6th edition but can not find this question in my book or on this website.It says on top of my page ch# 2 and page ref 2-7 but cant find it also how come you don't post question you just go to answers only . need to see question sometimes so I can find which edition it is in.

By Mr. Dychko on Thu, 9/6/2018 - 4:00 AM

Hi EddieG, thanks for the question. I would love to post the questions, but I've avoided that since it would be a copyright issue with the publisher since I didn't create the questions. Perhaps you can ask your teacher to photocopy just the problems from their 7th Edition text for your reference?
All the best,
Mr. Dychko

A baseball is hit almost straight up into the air with a speed of 25 m/s. Estimate

Find us on: