
A car traveling 75 km/h slows down at a constant just be "letting up on the gas." Calculate
- the distance the car coasts before it stops,
- the time it takes to stop, and
- the distance it travels during the first and fifth seconds.
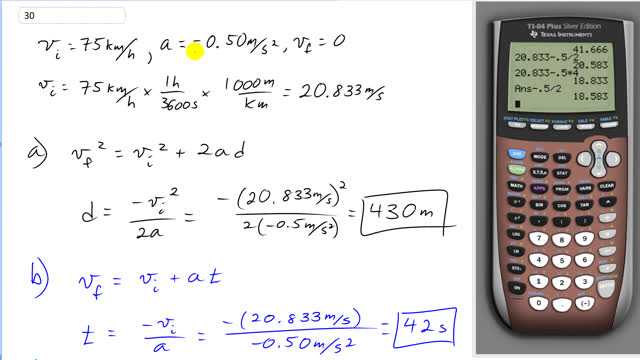
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. We start by writing down everything we know; the initial speed of the car is 75 kilometers an hour its acceleration is negative 0.50 meters per second squared and I have negative here to show that the acceleration is in the opposite direction to the velocity which we initially took to be positive and the final velocity is 0. We should convert this kilometers per hour into meters per second so that we can use them in the formulas along with this meters per second squared units of acceleration should always have mks units in your formulas—meters, kilograms, seconds. We'll divide by 3600 and multiply by a 1000 which is the same as dividing by 3.6 and we end up with 20.8333 meters per second. So we'll start with this formula for calculating the total distance that the car travels while it's coasting to a stop and we'll subtract v i from both sides squared and knowing that v f is zero by the way so that term just disappears and then flip the sides around and divide both sides by 2a as well so divide by 2a and you end up with distance is the negative of the initial velocity squared divided by 2 times the acceleration. So that's negative of 20.833 meters per second squared divided by 2 and then also divided by negative 0.5 and you get 430 meters with two significant figures. The total time it takes to stop is given by this formula here because we know the initial velocity and the final velocity and the acceleration; the final velocity being zero, and the initial can be subtracted from both sides and then divide both sides by a and then switch the sides around so you have the unknown t on the left and you get t is negative 20.833 meters per second divided by negative 0.5 meters per second squared for 42 seconds with two significant figures is the total time it takes for the car to coast to a stop. And then the distance traveled during the first second is the initial speed times one second plus one-half acceleration times time squared and that gives 21 meters with two significant figures and the distance traveled during the fifth second is a bit confusing because you have to make sure you calculate what the initial velocity is at the beginning of the fifth second which is the final velocity at the end of the fourth second so we'll use this formula here to find the final velocity at the end of the fourth second and that's the initial velocity we started with at the beginning of everything here which is 20.833 meters per second and then plus negative 0.50 meters per second squared times 4 seconds and after 4 seconds is done, the velocity is 18.33 meters per second and that is the initial velocity of the fifth second so we plug that in times by the 1 second because it's just during this single fifth second plus one-half times acceleration and times time squared giving you 19 meters overall with one significant figure. And we expect this 19 meters to be less than the 21 meters and it is which is good because the car's slowing down so the distance traveled during the fifth second should be less than the distance traveled during the first second so always do a reality check on your answers by the way just to make sure they make sense.
Hi,
I have a question that if the object has constant negative velocity, will the object speed up or slow down?
Hi m_iqbal, thanks for the question. The negative sign for velocity indicates direction only. It says nothing about whether the object is speeding up or slowing down. A negative velocity means only that the object is moving in the negative direction, which is typically to the left, although a person solving a problem is free to redefine the coordinate system by saying "I feel like making the negative direction to the right". It's a bit unusual to say "right is negative", but you do need to be prepared for this idea since occasionally I do say "let down be the positive direction", rather than the traditional "up is positive", when doing so simplifies the mathematics by avoiding so many negative signs in a formula.
A change in speed is given by acceleration, so your next question might be: does a negative acceleration mean the object is speeding up or slowing down. The answer here depends on whether the object currently has a negative velocity, or not. If the acceleration has the same sign as the velocity, it's speeding up. An acceleration with an opposite sign to the velocity means the object is slowing down. So, running through the list of possibilities: +a & +v => speeding up, -a & +v => slowing down, +a & -v => slowing down, -a & -v => speeding up. The last scenario is probably the one you'll want to take note of, where a negative acceleration means the object is speeding up when it already has negative velocity.
All the best,
Mr. Dychko
why is it velocity squared?