
Suppose you adjust your garden hose nozzle for a fast stream of water. You point the nozzle vertically upward at a height of 1.8 m above the ground (Fig. 2–40). When you quickly turn off the nozzle, you hear the water striking the ground next to you for another 2.5 s. What is the water speed as it leaves the nozzle?

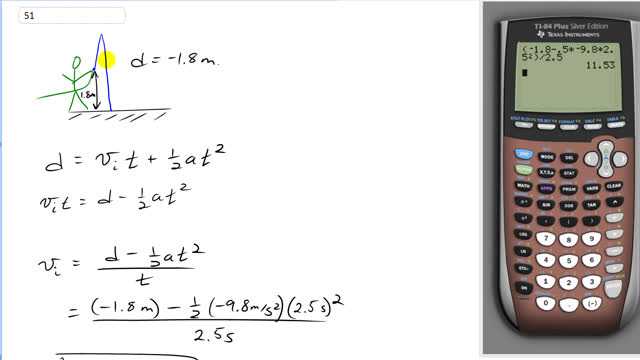
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. This garden hose sprays water straight up and it's positioned 1.8 meters above the ground and when the water launches from here, it hits the ground 2.5 seconds later. So the displacement of this water is gonna be negative 1.8 meters if we choose upwards to be the position direction and whenever in doubt about this negative or positive for displacement, you can always think of displacement as being the final position minus the initial position; typically, the letter y is used for this, you know, the y-axis being vertical so y final minus y initial and we have y final in this case being zero if this is a zero level here and then minus the initial position— minus 1.8 meters—above that giving us negative 1.8 meters so displacement is negative 1.8. We'll use this formula to solve for the initial speed and we'll subtract one-half at squared from both sides and we get this next line after we switch the sides around so that the unknown v i is on the left and then divide both sides by t and we get this formula for the initial speed. So we plug in our numbers; it's negative 1.8 meters displacement minus one and a half times negative 9.8 meters per second squared acceleration due to gravity times 2.5 seconds square that and divide by 2.5 for a total of 12 meters per second it must have been the initial speed of the water.