
An ideal gas expands at a constant total pressure of 3.0 atm from 410 mL to 690 mL. Heat then flows out of the gas at constant volume, and the pressure and temperature are allowed to drop until the temperature reaches its original value. Calculate
- the total work done by the gas in the process, and
- the total heat flow into the gas.
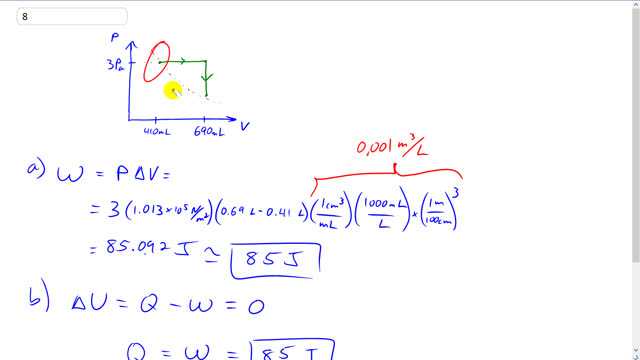
In order to watch this solution you need to have a subscription.
This is Giancoli Answers with Mr. Dychko. Here's a PV diagram of this process. The gas starts at three atmospheres of pressure at a volume of 410 milliliters and then it has an isobaric transition from this volume to this volume. So at constant pressure it's going to change from 410 milliliters up to 690 milliliters and it's during this phase that some work is going to be done because work is going to be pressure times change in volume. This is true whenever you have constant pressure and if pressure is changing and volume is changing well then you have to use calculus or else look at the area underneath the graph but for constant pressure you can just multiply this by change in volume and there's no work being done during this transition when it's iso-volumetric because there's no change in volume so there's no distance over which any force is being applied because that's what work is, force times distance. And then there's there is work being done when it goes back to the beginning but you know. We're told that it just, It just goes from here and then ends up here. So it doesn't go back to the beginning at all. But I drew this dotted red line. This is the isotherm that connects this point and this point because we're told that it changes its pressure once it gets to 690 millimeters to the point where it reaches the same temperature that it had originally. And so all points with the same temperature lie along these isotherms. These one over X reciprocal shaped lines. So, work done by the gas is, pressure times change in volume. The pressure is three times atmospheric pressures so three times 1.013 times ten to the five newtons per square meter times a change in volume which is 0.69 liters final volume minus 0.41 liters initial volume and then we have to convert that into a cubic metres so multiply by a one cubic centimeter per milliliter and then times by a thousand milliliters per litre and times by one cubic metre for every hundred, well one meter for every hundred centimeters to the power of three so that you cancel these cubic centimeters here, whether you do three fractions like this or one fraction like that it just depends on which conversion factors you happen to have memorized. Memorize that it's one cubic centimeter for every milliliter. In any case this works out to cubic meters after this is all said and done and we end up with 85 joules of work done by the gas. Change in internal energy is the heat absorbed by the gas minus the work done by the gas and that equals... that equals zero because it goes back to its original temperature. So we know that change in internal energy is three over two times n R times delta T. And since Delta T is zero that means this change in internal energy is zero because it returned back to its original temperature. And so that means the heat absorbed equals the work done and it's going to absorb 85 Joules.