VIDEO TRANSCRIPT

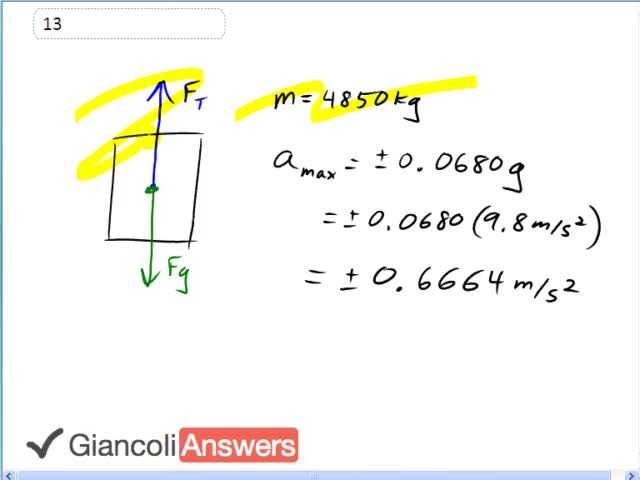
This elevator which has a mass of four thousand eight hundred and fifty kilograms has a cable exerting some tension force ‘FT’ upwards and gravity has a force downwards and the maximum acceleration this thing can experience in either direction, which is why I have a plus or a minus here, is zero point zero six eight times ‘g’. So let’s turn that into units of meters per second squared by multiplying it by nine point eight meters per second squared since that’s what ‘g’ is and we get the maximum acceleration up or down zero point six six six four meters per second squared. We use the net force formula to figure out the tension force. So we have net force as the upward forces which is tension minus the downward forces which is gravity in this case and then net force always is mass times acceleration according to Newton’s 2nd law. We’ll add force of gravity to both sides giving us that: ‘FT’ is ‘m’ times ‘a’ plus ‘f’ times ‘g’. ‘f’ times ‘g’ though is ‘m’ times ‘g’ so substituting that and we have ‘m’ times ‘a’ plus ‘m’ times ‘g’ and that’s what the ‘FT’ is. Factoring out the ‘m’ to make it look a little cleaner we have: tension force ‘FT’ is ‘m’ times ‘g’ plus ‘a’ and in the scenario where the acceleration is upwards we have ‘a’ greater than zero so we are taking the plus sign to begin with and then we’ll consider the negative case secondly. We have the tension force, this is going to be the maximum tension force because this is when the cable has to accelerate the elevator upwards and so it’s going to take more tension to do that than it will take to accelerate it downwards because gravity will do more of the work when it accelerates down. So we have: FT max is four thousand eight hundred fifty kilograms times nine point eight meters per second squared plus this design acceleration zero point six six six four meters per second squared and that gives fifty thousand seven hundred sixty two better written as five point zero eight times ten to the four Newtons is the maximum tension force. In the scenario where acceleration is less than zero now we’ll get the minimum tension force when the elevator is being dropped. So we multiply its mass by nine point eight meters per second squared minus zero point six six six four meters per second squared and this gives us forty four thousand two hundred and ninety eight which we’ll write instead as four point four three times ten raised to power four newtons will be the minimum tension force. In the 5th Edition the acceleration is a little different, it’s zero point zero six zero zero ‘g’s which gives us plus or minus zero point five eight eight meters per second squared. So the acceleration is less, which means the maximum force will be smaller and the minimum tension force will actually be a little larger than in this scenario. So we substitute the plus zero point five eight eight meters per second squared here giving a maximum tension force of five point zero four times to ten raised to power four newtons. Then we have minus zero point five eight eight giving a minimum tension force of four point four seven times ten to the four newtons for the 5th Edition.