VIDEO TRANSCRIPT

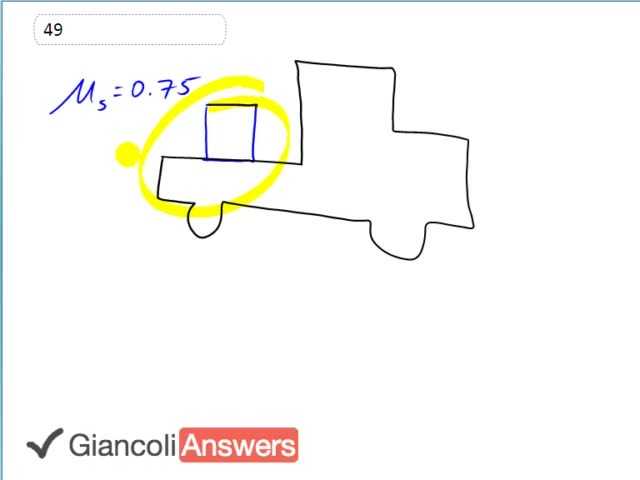
We have this crate in the back of a flat bed track and we need to know what is the maximum deceleration the truck can have and still not have the crate slide into the cab of the truck. We draw a free body diagram of the crate and when the truck is decelerating there will be friction going in this direction and there is of course a normal force upwards and a normal force downwards. And the normal force is going to equal gravity. But first we’ll say the Newton second law is that the friction force, then we’ll put a negative in front of it because it’s in the negative direction, we’ll say this is the positive X direction to the right, negative friction force equals ‘m’ times ‘a’ and we know also the friction force equals co-efficient of static friction times ‘FN’ and FN’ equals to the gravity because there is n vertical acceleration. And so we could say friction is ‘µs’ times ‘m’ times ‘g’. From this equation we can say that the friction force equals negative ‘m’ times ‘a’, multiply both sides by negative one. And now we have friction force equaling negative ‘m’ times ‘a’ and also equaling ‘µs’ times ’m’ times ‘g’, so those two are equal. We have negative ‘m’ times ‘a’ equal ‘µs’ ’m’ times ‘g’, ‘m’s cancel on both sides and we will multiply both sides by negative one leaving us with positive ‘a’ equals negative ‘µs’ times ‘g’. That gives us negative zero point seven five times nine point eight meters per second squared which is negative seven point four meters per second squared which is the maximum deceleration the truck can have before the crate starts sliding.