VIDEO TRANSCRIPT

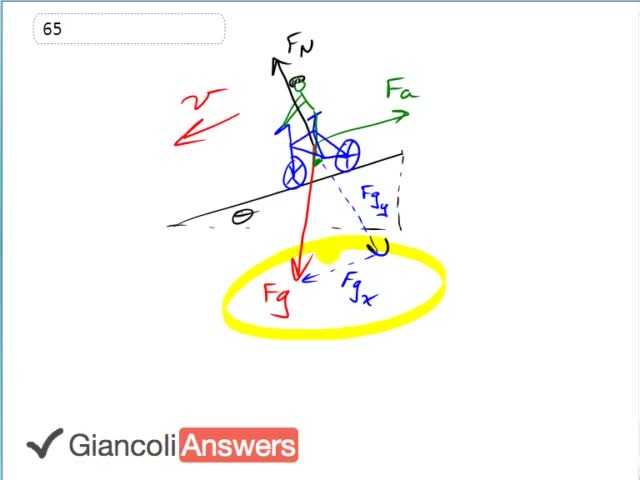
When the cyclist is going downhill the free body diagram looks like this. We have the X-component of gravity along the ramp pulling him down and the air friction up the hill that’s holding him back and these two are equal since the speed is constant at six kilometers an hour. And from this we can figure out what the air friction will be. Let’s write down some more information we know: mass is sixty five kilograms and the hill incline is six degrees and ‘v’ is six kilometers per hour which normally I would convert to meters per second but it turns out to be an irrelevant piece of information so all we need to know is that the speed is constant, that’s what’s important. And since there is no acceleration we can say that the air friction ‘Fa’ equals the X-component of gravity ‘Fgx’ being the opposite leg of this gravity force triangle. Since it’s the opposite we have sine theta to find it. And that’s about all we can do with that picture. And then the second scenario is where the cyclist is climbing back up the hill, we’ll just draw him as a box it will be faster. And the force that the cyclist needs to apply and there is gravity downwards with components into the ramp and along the ramp, that’s ‘Fgx’ there. And you have air friction holding him back which is down the ramp since the velocity in this new scenario is up the ramp so we have ‘Fa’ going down and is also normal force but that’s actually not important to you either. What is important is to know this ‘Fa’ is the same ‘Fa’ as it was in the top scenario where it’s going downhill. So from this picture Newton’s second law would be that the force applied by the cyclist up the hill has to equal the total forces working against them. That’s: ‘Fa’, air friction, plus the ‘Fgx’ and we know that’s true because his velocity is constant. And ‘Fc’ then is equal to ‘m’ times ‘g’ sine theta where I made a substitution for ‘Fa’ which we know from the first part of the question plus ‘m’ times ‘g’ sine theta again, because ‘Fgx’ is the opposite leg of this gravity force triangle where we can put theta here and here. so then the force the cyclist has to exert is two times ‘m’ ‘g’ times sine theta and that is two times sixty five kilograms times nine point eight newtons per kilogram times sine six degrees and that equals one hundred thirty newtons.