VIDEO TRANSCRIPT

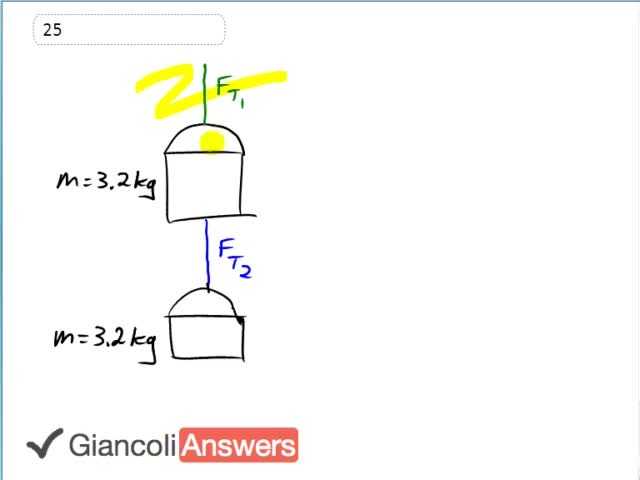
Our job is to figure out the tension forces in this segment of rope which is holding the first bucket and then the second segment of rope which is holding only the bottom bucket. Let’s draw the free body diagram from the perspective of the top rope, we can think of this whole apparatus all two buckets together as one box that I’ve drawn in blue here. ‘FT1’ is supporting that whole system and there is gravity pulling down as well and then we have ‘Fg1’ and this picture has the arrows same length up and down because it’s at rest in part a, and let’s figure it out then. We know that ‘FT1’ which is the up force has to equal the down force in order for this bucket to not accelerate and the down force is going to be the total mass which is two ‘m’ since we are modeling the whole two buckets as a single block from the perspective of the top rope. So that’s two ‘m’ times ‘g’ is going to be the force of gravity downwards. So ‘FT1’ is: two times three point two kilograms times nine point eight newtons per kilogram giving us sixty two point seven two newtons which will in two significant figures, sixty three newtons. From the perspective of the bottom rope we’ll have to draw another picture. It’s going to have only one bucket that it has to support, only the bottom bucket is supported by this tension force two and so its free body diagram will have this box with only mass ‘m’. And we’ll have ‘Fg2’ going downwards and ‘FT2’ going upwards. So in this case we have ‘FT2’ equals ‘Fg2’ downwards, since there is no acceleration they have to be the same up and down so that’s ‘m’ times ‘g’ and then we know that ‘FT2’ equals three point two kilograms times nine point eight newtons per kilogram, it’s going to be half of our answer for ‘FT1’. That’s thirty one Newtons. Now in part b, we are going to have the buckets accelerating upwards and our free body diagrams will have the up arrow longer than the down arrow. So redrawing the system for ‘FT1’ this box has mass two ‘m’ because from the perspective of the top rope it’s supporting both buckets. And we have ‘Fg1’ downwards and the up arrow is longer than the down arrow since the buckets are accelerating upwards. So we know that ‘FT1’ which is the total up force minus ‘Fg1’, total down force, equals mass times acceleration and in this case we are going to write two ‘m’ which is the mass of this system. And then solving for ‘FT1’ by adding ‘Fg`’ to both sides, gives us ‘FT1’ is two ‘m’ times ‘a’ plus ‘Fg1’ where ‘Fg1’ is two ‘m’ times ‘g’. And we can see that two ‘m’ is a common factor so let’s factor that out, ‘FT1’ is two ‘m’ times ‘a’ plus ‘g’ so that’s two times three point two kilograms times one point six zero meters per second squared, acceleration upwards, plus nine point eight meters per second squared. Notice that ‘g’ is always positive nine point eight even though the acceleration due to gravity is directed downwards this letter ‘g’ is always this positive number and if you want to say that it’s down you just have to put a negative sign in front of it. This works out to seventy three Newtons, the tension force in the top rope. For ‘FT2’ we’ll say, ‘FT2’ minus ‘Fg2’ is ‘m’ times ‘a’. And I mean a single ‘m’ times ‘a’ because from a perspective of the bottom rope it’s supporting only a mass ‘m’. So here we have ‘FT2’ and ‘Fg2’ and this block or the bottom bucket in other words has mass ‘m’. So ‘FT2’ is: ‘m’ times ‘a’ plus ‘FT2’ which is ‘m’ times ‘a’ plus ‘m’ times ‘g’ factor out the ‘m’ we have ‘m’ times ‘a’ plus ‘g’ and that is three point two kilograms times one point six meters per second squared plus nine point eight meters per second squared giving us thirty six newtons for the bottom rope. In the 5th Edition the masses are slightly different, so we have three point zero kilograms instead and we’ll make substitutions everywhere we see three point zero, and the 5th Edition answer is, fifty nine newtons for the top strand and then twenty nine newtons for the bottom strand when the buckets are at rest. And then when the buckets are accelerating we’ll have three point zero here giving a top strand force of sixty eight newtons and then bottom strand when the buckets are accelerating upwards we’ll have a force of thirty four Newtons in the 5th Edition.