VIDEO TRANSCRIPT

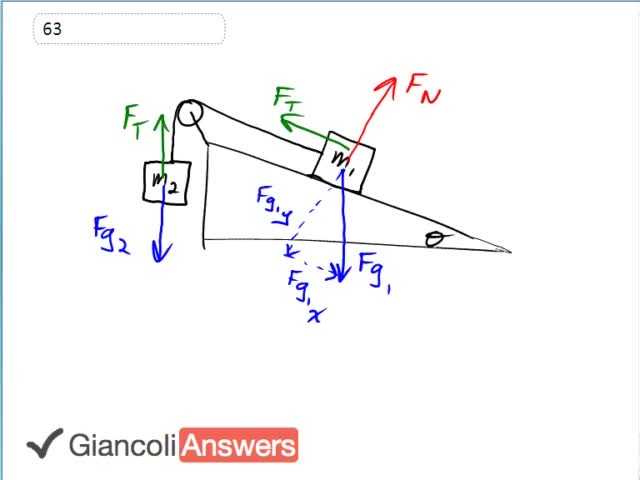
Our job is to figure out the acceleration of the system, and we are assuming that there is no friction. We are going to define a coordinate system in perhaps an odd looking way, we are going to say this direction is positive, this is the X-positive direction along the curve. So if ‘m2’ goes up or ‘m1’ goes down the incline that direction is going to be positive. Now we are going to make simplifying picture so let’s forget about these tension forces, they are equal and in opposite directions and we can actually instead think of this as a system of two masses that are horizontal, we have ‘m2’ on the one side and ‘m1’ on the other side and it’s being pulled in two directions, it’s being pulled to the right by a force of ‘Fg1x’. So that’s the component of gravity which is pulling ‘m1’ down the plane and so that’s the force we’ve written here and then pulling it the other way along this path is ‘Fg2’ pulling ‘m2’ down and on this picture we’ll imagine it to the left so this is ‘Fg2’. And this is going to make life easier because we’ll think of these two forces as acting on a single system. We’ll think of ‘m1’ and ‘m2’ as a one big box, with only two forces on it, ‘Fg1x’ is the magnitude of the force on the right and ‘Fg1’ is the magnitude of the force on this yellow large box to the left. That’s the way we are going to think of it because the system accelerates together. So we have ‘Fg1x’ to the right minus ‘Fg2’ to the left equals the total mass times this acceleration of the system and we can make substitutions for each of these, the X-component of gravity on mass one we are going to use sine since sine gets us the opposite leg of these gravity force triangle. So we’ll say ‘Fg1x’ is actually: ‘m1’ times ‘g’ sine theta minus ‘m2’ times ‘g’ the total gravity on the hanging mass. And that equals the total mass of ‘m1’ plus ‘m2’ times ‘a’ and we’ll solve this for ‘a’ by dividing both sides by ‘m1’ by ‘m2’ so we have ‘a’ equals ‘m1’ times ‘g’ sine theta minus ‘m2’ times ‘g’ over ‘m1’ plus ‘m2’. The assumption we made here with making it a system all along one line is valid when there is no friction. If there is friction then you can’t use this simplifying picture because perhaps there is friction only on mass one and then that’s a force that can’t be modeled this way because it’s not acting on the whole system it’s acting only on this particular part of the system and so you’d have to draw a free body diagram for each mass separately and do it that way. There is a question coming up pretty soon where I do that. It’s number sixty four in the 6th Edition or sixty two in the 5th Edition In any case let’s get part b done. And so we can see here that if this ‘m1’ times sine theta is greater than ‘m2’ then the acceleration will be positive. By factoring up the ‘g’ and you can really see what I’m talking about here so we have ‘g’ times ‘m1’ sine theta minus ‘m2’ all over ‘m1’ plus ‘m2’ so if this numerator is positive that means it’s accelerating down the ramp because we define positive as down the ramp. So that’s what we’ll say in part b. If ‘m1’ sine theta is greater than ‘m2’ then acceleration is greater than zero and the opposite is also true. So if ‘m1’ sine theta is less than ‘m2’ then ‘a’ is less than zero and it’s accelerating up the ramp because we said to the left is negative.