how do you know g is positive?

Hi dorfte, "g" is technically always positive. It's meant to represent the magnitude of the acceleration due to gravity. This means the acceleration due to gravity (not just its magnitude), in a traditional coordinate system where down is negative, is -g (note the negative in front of the "g").

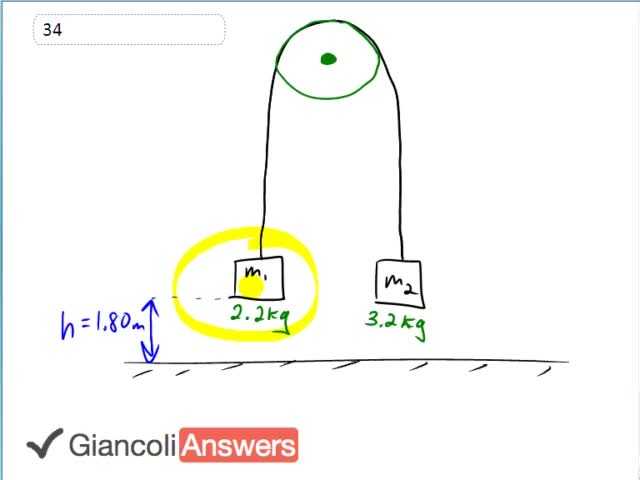
In my re-drawing of the Attwood machine in this video, I made left negative, and right positive, which is conventional. I like to make negatives 'explicit', which means I put them directly into the equation, instead of having them hidden within variables, which is why I wrote $F_2 - F_1 = m_2g - m_1g$ at about 2:15 in the video.

Why don't you take Force Tension into account. ANSWER QUICKLY PLEASE. Thank You

Where video plz???