VIDEO TRANSCRIPT

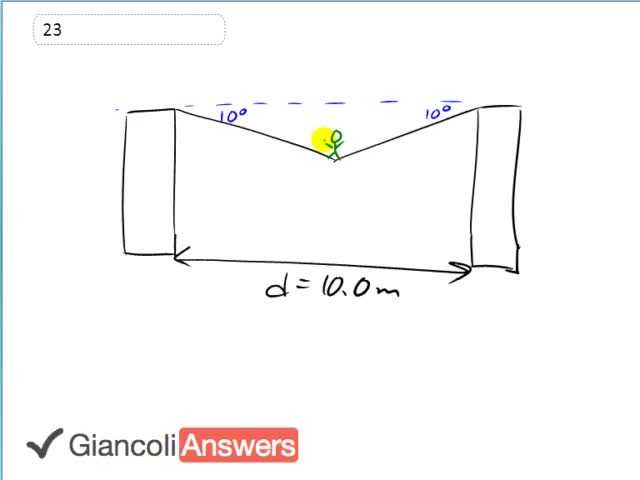
We have the tight rope walker Arlene right in the middle of the tight rope between these two buildings and we’ve put the information on this picture, most of it anyway, the tight rope has an angle of ten degrees below horizontal, the buildings are ten meters apart although that piece of information is actually not needed and while Arlene is not accelerating right now, so that means that the force downwards due to gravity is balanced by an upwards force and that’s exerted by the tight rope. I’m going to label this as two times the Y-component of the tension force and we’ll have to zoom in on this spot and draw another picture to explain why. So we are zooming in on that spot right there. There is going to be a tension force to the right, a tension force to the left, and gravity downwards. So I’m drawing all the forces on the rope at this spot here and these blue arrows should be the same length. And we are told that this is ten degrees here, so we can also say this is ten degrees and you need to see that the Y-component of this tension force, so this blue arrow represents the tension force directed along the rope ‘FT’, and it has a Y-component ‘FTy’, which is ‘FT’ times sine of ten degrees. And there’s two of them there is one on the left side here as well and so this explains the times two better, this is ‘FTy’ as well. Now these two Y-components forces upwards have to equal the gravity downwards so let’s say that with algebra. We have: two times the Y-components and we’ve said that the Y-component is ‘FT’ times nine theta that equals force of gravity which is ‘m’ times ‘g’, and we’ll solve for ‘FT’ by dividing both sides by two times sine theta. So: ‘Ft’ is ‘m’ times ‘g’ divided by two sine theta and that gives us fifty point zero kilograms times nine point eight newtons per kilogram divided by two times sine of ten degrees giving us the tension force of one point four one times ten raised to power three newtons.