
In order to watch this solution you need to have a subscription.
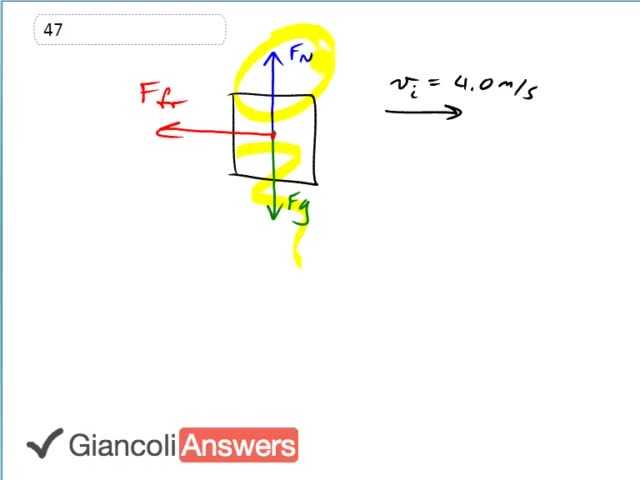
Here is a free body diagram of this block, it will gravity pulling it down towards the floor and a normal force upwards of equal magnitude to the gravity since it is not accelerating vertically and there will be this friction force going backwards opposing its motion which initially is four meters per second to the right. We also know that the coefficient of kinetic friction is zero point two and the final speed is zero meters per second because the question is how far will this block go. We are going to have to figure out first ‘a’, that’s acceleration and then after knowing that acceleration we will be able to figure out the distance. And we’ll find ‘a’ using forces. So say the friction force which is the only horizontal force equals ‘m’ times ‘a’ because since it’s the only one it is the net force. And then we also know the friction force equals: coefficient of friction times the normal force and the normal force is equally gravity since there is no vertical acceleration. So if friction equals ‘µ’ times ‘m’ times ‘g’ and friction equals ’Ffr’ it means that the two are equal. And so we’ll say: ‘m’ times ‘a’ equals coefficient of friction times ‘m’ times ‘g’, ‘m’s cancel telling us that ‘a’ equals coefficient of friction times which is zero point two times nine point eight meters per second squared which is one point nine six meters per second squared and I’m going to introduce a negative sign because we know from our picture that this acceleration is in the negative direction, it’s to the left. And now we’ll figure out how far this block will go. We’ll use the formula ‘vf’ squared equals ‘vi’ squared plus two ‘a’ times‘d’. We know that the final speed is zero then we’ll subtract ‘vi’ squared from both sides and so we have two ‘a’ times ‘d’ equals negative ‘vi’ squared and then divide both sides by two ‘a’ to solve for ‘d’. So we get ‘d’ equals negative ‘vi’ squared over two ‘a’ which is negative four point zero meters per second squared divided by two times negative one point nine six meters per second squared giving us a distance of four point one meters.
Hmmm... I guess I'd have to say that since the friction force increases with mass, and the net force also increases with mass, that mass doesn't matter since it increases both by the same factor. It's like if you were to equate a crowd of 1000 people in New York with two times the number of people in a SmallVille crowd (which means the SmallVille crowd as 500 people). If Lady Gaga shows up, both crowds increase by maybe 10 times, but it's still true that the New York crowd is 2 times the SmallVille crowd. The Lady Gaga factor doesn't change the equality, nor the fact that the New York crowd is twice the size of the SmallVille crowd. It cancels, like the mass. Acceleration equals the coefficient of friction times acceleration due to gravity, regardless of what mass both sides are multiplied by.
hello,
I can understand algebraically why the masses cancel, but could you explain it conceptually?
Thanks!
haha. thanks. I like the analogy. Another one I thought of is just that when you drop the hammer and the feather on the moon (no g) they fall at the same rate (mass cancels). Yours is way more fun. thanks.