
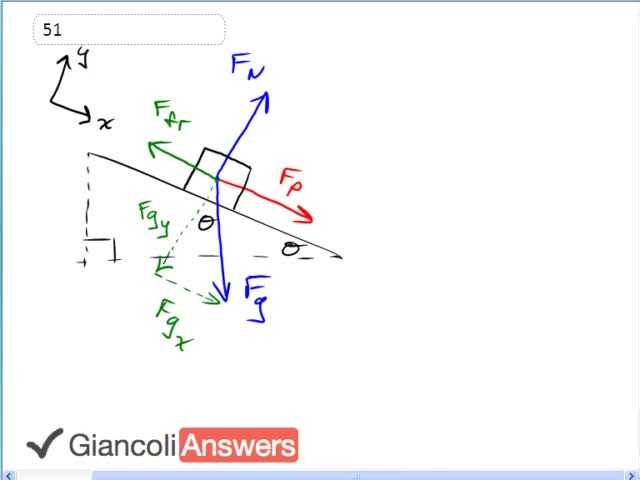
Please ignore the red force arrow in the diagram.
In order to watch this solution you need to have a subscription.
This is a great question but it should really be labeled level three difficulty. There are quite a few steps, the first step will be to figure out what is the coefficient of kinetic friction in terms of acceleration down the ramp and we’ll be using the scenario where there is friction when we do that. And then we’ll find an expression for the acceleration with friction in terms of the acceleration without friction since we know how this final speed today at the bottom of the ramp knowing that the speed with friction is half of what it would be without friction. Let’s continue to write down what we know here: twenty eight degrees is the angle of incline. The kinetic coefficient of friction is what we want to find and we know that the final speed in scenario one with friction equals half of the final speed in scenario two without friction. And we know that the initial speed in both scenarios is zero. So with friction, let’s write down Newton’s second law and find an expression for the co-efficient of friction, so we call this equation one. We know that ‘Fgx’ to the right, and we have our co-ordinates system defined so the positive is down the ramp, minus the friction going up the ramp equals mass times acceleration. We’ll put a subscript one on that acceleration to denote that it’s the acceleration in this scenario where there is friction, scenario one. We know the friction force, we are going to substitute for those force terms here, friction force is ‘µk’ times ‘FN’, where ‘FN’ is the Y-component of gravity because there is no acceleration perpendicular to the ramp and so it must be that this normal force equals the Y-component of gravity. So algebraically, ‘Fgy’ is the adjacent leg of the gravity force triangle and so we use cosine to get it. So we have the friction force which is ‘µk’ times ‘m’ times ‘g’ cosine theta where ‘m’ times ‘g’ is force of gravity, cosine theta gets that adjacent leg. ‘Fgx’ is ‘m’ times ‘g’ sine theta because it’s the opposite leg of the gravity force triangle. And then we’ll make substitutions into equation one, let’s call it one version b: ‘m’ times ‘g’ sine theta minus ‘µk’ times ‘m’ times ‘g’ cosine theta equals ‘m’ times ‘a1’, the ‘m’s will cancel and we can solve for ‘µk’ so we have ‘µk’ times ‘g’ cosine theta equals ‘g’ sine theta minus ‘m’ times ‘a1’ and then we’ll divide both sides by ‘g’ cosine theta giving us ‘µk’ is ‘g’ sine theta minus ‘a1’ divided by ‘g’ cosine theta. And this would be our answer if we knew what ‘a1 ‘is. And the rest of this question will involve figuring out ‘a1’ so that we can plug it into here and get the coefficient of friction since we know both of these things. So first we’ll express ‘a1’ in terms of final speed in scenario one because that’s something we have a relation in between the two scenarios, express ‘a1’ in terms of ‘v1f’ and we use this formula: ‘v1f’ squared equals ‘v1i’ squared plus two ‘a’ times ‘d’, that’s the usual formula, the initial speed being zero. And I’m just making up some distance to the end of the ramp from the starting position and it doesn’t matter where that is because it’s going to be the same for both the friction and frictionless scenarios. And from this we can solve for ‘a’ by dividing both sides by two‘d’: ‘a1’ equals ‘v1f’ squared over two‘d’. We know that ‘v1f’ is ‘v2f’ over two and so we’ll make that substitution now, we’re finally relating the scenario with friction to the one without friction because when there's no friction we will actually be able to calculate the acceleration. So this is ‘v2f’ over two squared over two‘d’. So ‘v2f’ over two gets squared meaning that we’ll have a denominator four up here and this all works out to ‘v2f’ squared over eight ‘d’ because the four resulting from squaring that gets multiplied by two down here giving eight. If I ever leave out some steps you want to see make sure you leave a comment below the video. So now we know ‘a1’ in terms of the final speed without friction, that’s what ‘v2’ represents. So let’s calculate that. In this case we have Newton’s laws without friction, that’s scenario two, we have the ‘Fgx’ equals ‘m’ times ‘a2’ because there is no friction force now so only ‘Fgx’ is on the free body diagram in the scenario without friction. And from this we can say: ‘m’ times ‘g’ sine theta equals ‘m’ ‘a2’, ‘m’s cancel giving us: ‘a2’ is ‘g’ sine theta and then knowing ‘a2’ we’ll be able to find ‘vf2’. We’ll use the formula: ‘v2f’ squared equals ‘v1f’ squared plus two ‘a’ times ‘d’, ‘v1f’ squared being zero. What we actually care about is ‘v2f’ squared so that’s: two times ‘g’ sine theta, and making a substitution we can write ‘g’ sine theta times‘d’. And this will get plugged in way up here because now we’ll be able to find ‘a1’ and then knowing ‘a1’ we can find coefficient of friction. So it is all related. We know that ‘a1’ equals two ‘g’ sine theta‘d’ over eight ‘d’, the top of this is the expression ‘vf22’ because this expression is ‘vf22’. And in ‘a1’ we have the top which is ‘vf22’ and so we just make this substitution directly and simplify, that makes: ‘g’ sine theta over four, seeing that the ‘d’s cancel and the two over eight reduces to one over four and now we can substitute into our ‘µk’ formula. So it’s ‘g’ sine theta minus ‘a1’ over ‘g’ cosine theta and we’ll substitute for ‘g’ sine theta over four in place of ‘a1’ now. ‘g’ sine theta minus ‘g’ sine theta over four all over ‘g’ cosine theta. First o all the ‘g’s cancel and the top is sine theta minus a quarter sine theta living us with three quarters sine theta on the top. So three quarters sine theta all divided by cosine theta, and sine theta divided by cosine theta is tangent theta so we have three quarters times tangent theta. The answer to our whole question is that the coefficient of friction is three quarters tangent theta. Amazingly simple answer for such a complicated question. So it’s three quarters of tangent twenty eight, and that is zero point three nine eight seven eight which we should write with two significant figures as zero point four zero.