VIDEO TRANSCRIPT

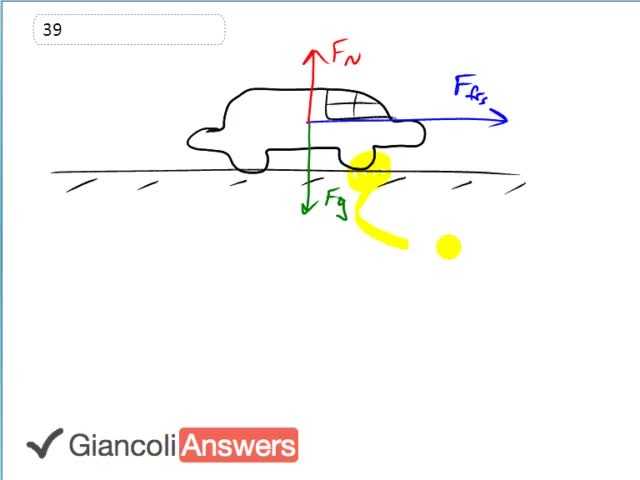
We’re going to figure out what maximum acceleration is possible given a particular coefficient of static friction. And it’s interesting to think of the maximum acceleration being constrained by friction. You normally think of the engine’s number of cylinders as being the determining factor for acceleration. Well there is a maximum strength or horsepower of the engine that’s possible and beyond that you won’t get anymore acceleration because the limiting factor will be the friction between the tires and the road. So if you had the biggest engine in the world in this car what would its acceleration be knowing that the limit is based on friction? That’s what we are going to figure out. The static friction which is what’s exerting a force forward on a car the force of friction due to the road on the car is ‘μs’ times ‘FN’ and the normal force is equal to ‘mg’ since it’s not accelerating upwards. The static friction force also equals ‘ma’ because that’s Newton’s second law and there’s only one force in the horizontal direction. And so that is the net force and so it equals ‘ma.’ and so we can equate these two parts and say that ‘μs’ times ‘mg’ equals ‘ma’. Let’s divide both sides by ‘m’ we have ‘a’ equals ‘μs’ times ‘g’ which is zero point eight zero times nine point eight meters per second squared and that equals seven point eight meters per second squared is the maximum possible acceleration for these tires on this road.