VIDEO TRANSCRIPT

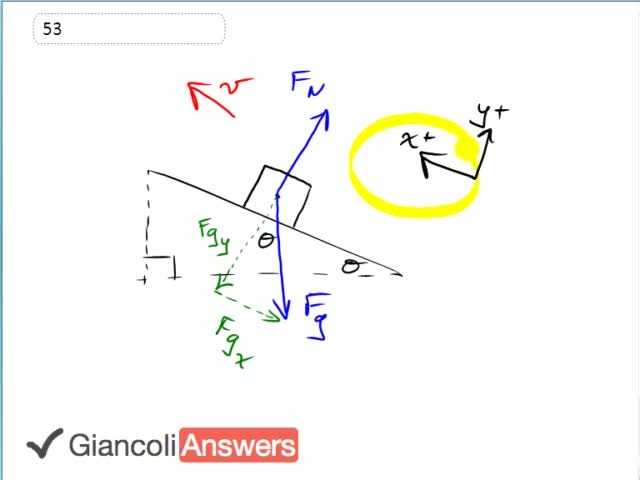
This carton is pushed up the ramp with some initial speed of three minute per second. We are going to define our coordinates system as X positive up the ramp just so we can say that the initial velocity is positive. So that means ‘vi’ is positive three point zero meters per second. We are told that the angle of incline is twenty two degrees, there is no friction and our job is to figure out how far up the ramp will it go and part b, figure out how long it will take to go from the starting position up the ramp and back to the starting position, so the time for the full around trip, that’s part b. So in a, we need to figure out the acceleration of the box first and then from that figure out the distance it will go. We’ll use Newton’s second law, we have that the X-component of gravity is the only one along the ramp and its negative because it is pointing to the right and we defined positive as to the left. And so negative ‘Fgx’ equals ‘m’ times acceleration 'a'. ‘Fgx’ is the opposite leg of this gravity force triangle and so we’ll use sine to get it where ‘Fg’ is ‘m’ times ‘g’. ‘Fgx’ then is going to be ‘m’ times ‘g’ sine theta and that equals ‘m’ times ‘a’, the ‘m’s cancel and meaning that we have now solved for ‘a’. We have ‘a’ equals negative ‘g’ sine theta. We’ll substitute that into our kinematics formula so we have: ‘vf’ squared equals ‘vi’ squared plus two ‘a’ times ‘d’ and we use this one because we know everything in it except for ‘d’. We know the final speed at the top of its trajectory zero and we know the initial speed, we know the acceleration now. So two ‘a’ times ‘d’ equals negative ‘vi’ squared, dividing those sides by two ‘a’ giving us that ‘d’ equals negative ‘vi’ squared over two ‘a’ and ‘a’ is negative ‘g’ sine theta so we’ll substitute that in now so we have negative ‘vi’ squared over two times negative ‘g’ sine theta, we have ‘vi’ squared over two ‘g’ sine theta. And we plug in numbers and we get our answer, so ‘d’ is three point zero meters per second squared, that’s the initial speed, divided by two times nine point eight meters squared times sine twenty two. That equals one point two two five eight meters which we’ll round to two significant figures, one point two meters up the ramp is as far as it will go. In part b, we use the formula: ‘d’ equals initial speed times time plus one half ‘a’ times ‘t’ squared because we know all the things in here apart from ‘t’. We know that the displacement is zero because it’s going to return to its starting point and this means we can divide both sides by ‘t’ and so we have: one half ‘a’ times ‘t’ equals negative ‘vi’ because we’ll take it to the other side of the equation. And now we can multiply both sides by two and divide by ‘a’ and this will solve for ‘t’. So we have: ‘t’ equals negative ‘vi’ times two divided by ‘a’, ‘a’ being negative ‘g’ sine theta. And the negatives will cancel so we have; two ‘vi’ over ‘g’ sine theta and we can plug in the numbers to get our answer. So we have two times three point zero meters per second divide by nine point eight meters per second squared times sine twenty two giving one point six seconds for it to do a round trip up the ramp and then back to the starting point.