VIDEO TRANSCRIPT

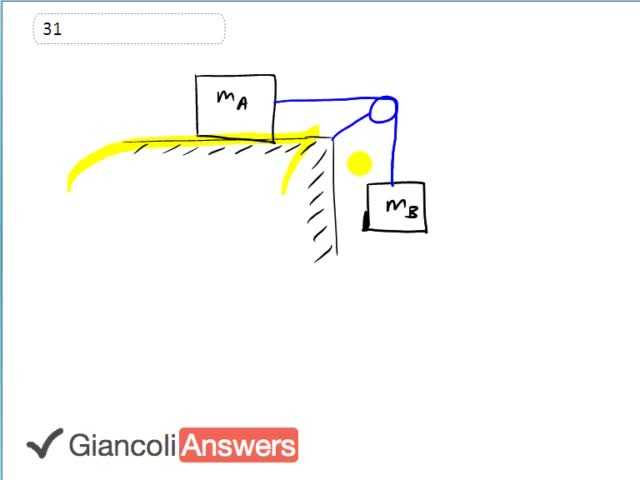
Given the set up of two boxes we need to figure out the free body diagram on each assuming that this surface is frictionless and the pulley is friction and there’s no mass in the cord and so on. Let’s try mass a first. There’ll be a normal force exerted by the surface that it’s on, there will be gravity downwards as well, and there’s the tension in the cable pulling it to the right. And then mass b will have only two forces on it, it will have the tension force pulling it upwards and gravity downwards. Now we should distinguish these two gravities, there’s s force of gravity on block a and force of gravity on block b. they will be different since the masses of the blocks are potentially different. The tension force though requires no subscript because it will be constant throughout the length of this rope so the tension experienced by block a will be the same as the tension experienced by block b because it’s all the same rope and no friction in the pulley. And in part b we have to figure out algebraically what will be the acceleration of the system and also what is the tension force. So consider block a, the Newton's second law will be that the tension force equals mass times acceleration. The tension force is the only force horizontally speaking and so it is the net force and net force is mass times acceleration. And for block b we’ll say that the force of gravity on block b minus the tension force equals mass of b times acceleration. I wrote the tension force as minus because I’m defining the coordinate system as X is positive to the right but Y is positive downwards. Positive is to the right and downwards. With this set up we can say that the tension force is ‘m’ times ‘a’ times acceleration. These accelerations don’t require subscripts because since we’ve defined the coordinate system this way obviously they’ll have the same magnitude because of the coordinate system we have. The accelerations they’re connected by a rope so the accelerations will be the same amount and because of our choice of coordinate system both the accelerations will be positive. So we’ve made the acceleration of block a and b exactly the same in terms of magnitude and sign so we can forget about any subscripts here. This allows a direct substitution from this first equation into the second one. The equation for b: force of gravity ‘FgB’ minus ‘ma’ times ‘a’ equals ‘mb’ times ‘a’. And we’ll substitute for force of gravity on block b that’s ‘mb’ times ‘g’ minus ‘ma’ times ‘a’ and we’ll have to solve for acceleration. We have ‘mb’ times ‘a’ plus ‘ma’ times ‘a’ equals ‘mb’ times ‘g’. Factoring out the ‘a’ we have ‘a’ times ‘ma’ plus ‘mb’ equals ‘g’ times ‘mb’. Divide both sides by ‘ma’ plus ‘mb’ and we end up with acceleration is: acceleration to the gravity ‘g’ times ’mb’ divided by ‘ma’ plus ‘mb’. So that’s one answer. And the tension force we know is ‘ma’ times ‘a’, so that’s ‘g’ times ‘ma’ times ‘mb’ all over ‘ma’ plus ‘mb’. We can say look at this acceleration and say does it make sense? The denominator says as the masses increase the acceleration will decrease and that does make sense because if you have really heavy blocks you can expect that the acceleration will be smaller because it’s harder to accelerate massive objects. But on the other hand, if mass b itself gets really large, that will increase the acceleration because it’s the whole source of the tension because it’s what pulling the system down and to the right and so as mass b increase acceleration will increase and the equation also reflects that by having mass b and the numerator.