VIDEO TRANSCRIPT

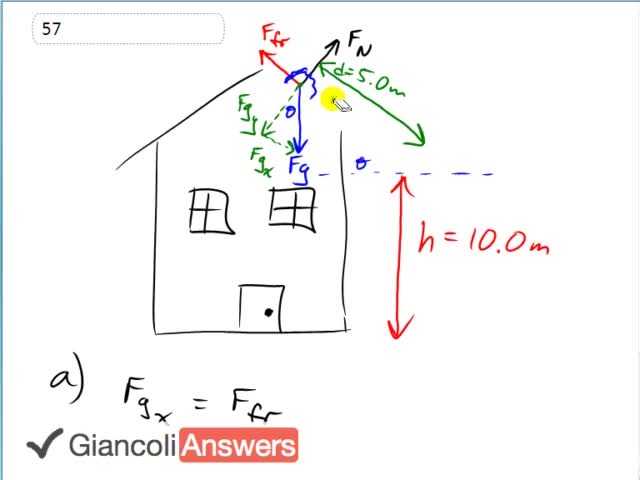
So in this question in part a we are going to say that this chunk of snow has to stay on the roof and what should the coefficient of static friction be in order to make sure that it stays there? And then part b we’ll say that the snow melts a bit so that the static friction coefficient is reduced and it’s too low and it starts to slide and it goes five meters to the edge of the roof. And then what will it’s speed be by the time it gets to the edge of the roof? Then part c is knowing that it’s going to fall ten meters what will it’s speed be by the time it hits the ground? Okay in part a we’ll say that the X-component of gravity equals the friction force, that has to be true in order for the chunk of snow to be stationary. And the X-component of gravity is going to be ‘mg’ times sine theta, ‘mg’ being the force of gravity and sine theta because the X-component is the opposite leg of that gravity force triangle. The friction force is the coefficient of static friction times ‘Fn.’ and ‘Fn’ is equal to the Y-component of gravity because there is no acceleration perpendicular to the roof. So we have ‘μs’ times ‘mg’ cosine theta that gets the adjacent leg of the gravity force triangle. And so ‘μs’ times ‘mg’ cosine theta equals ‘mg’ sine theta, substituting into this equation trying to solve for ‘μs’ the ‘m’s cancel and so do the ‘g’s and we’ll divide both sides by cosine theta as well giving us: ‘μs’ equals sine theta over cosine theta which is a trigonometric identity, tangent theta. And the roof is inclined at thirty degrees so theta equals thirty degrees so that means the minimum coefficient of static friction required to prevent slipping is zero point five eight tangent of thirty degrees. In part b we’ll say that the X-component of gravity minus friction equals ‘m’ times ‘a’ and we’ll have to figure out what ‘a’ is and then say that with an initial speed of zero and given five meters of distance traveled with this acceleration what will the final speed be? We’ll substitute for each of these things using the same logic we had before: ‘Fgx’ was ‘mg’ sine theta and friction is the coefficient of kinetic friction times ‘mg’ cosine theta, all of that equals ‘m’ times ‘a’ and we’ll cancel the ‘m’s so this means that the acceleration equals ‘g’ times in bracket sine theta minus ‘μk’ times cosine theta. Putting in a number there we have ‘a’ equals nine point eight meters per second squared times sine of thirty which is zero point five minus zero point two times cosine thirty giving an acceleration of three point two zero two six meters per second squared. Now the kinematics formula we use is this one: final speed squared equals initial velocity squared plus two ‘a’ times ‘d’, the initial velocity being zero and this means that ‘Vf’ is the square root of two ‘a’ times ‘d’ which is the square root of two times three point two zero two six meters per second squared times five meters and this gives a final speed of five point six five nine one, written with two significant figures as five point seven meters per second. So that’ll be the speed when it is at the edge of the roof. Part c says: after it slides off the roof what will its speed be just as it hits the ground? We are going to have to take this five point seven and turn it into components. So we’ll have this glob of snow here and it has an initial velocity of five point six five nine one and it’s going at an angle of thirty degrees with respect horizontal because that’s the pitch of the roof and it’ll have an X-component and a Y–component and the X-component will stay constant and the Y-component is going to be changing due to gravity. So we’ll say: the final speed at the ground that we are trying to find ‘Vfx’ is going to equal the initial X-component because there is no acceleration horizontally and so that’s going to be the initial velocity times cosine thirty because we are finding the adjacent leg of this velocity triangle and this gives us five point six five nine one meters per second times cosine thirty which is four point nine zero one meters per second. So put that in our back pocket for future reference we are going to use that later and we’ll switch over to the Y-component. We know how far it falls, we know the initial velocity and we know the acceleration so this is the ticket to answering what the final Y-component will be. It’s going to fall ten meters, the acceleration will be due to gravity nine point eight down. By the way for convenience I’m saying that Y is positive in the downwards direction. We’ll have to calculate the initial Y-component of the velocity in order to substitute into this formula, that’s the only thing we don’t know the number for at this point. So the initial Y is: the initial velocity times sine theta. Referring back to this triangle we are finding this green vertical component right now opposite legs so we use sine: five point six five nine one meters per second times point five that’s what sine thirty is. And we’ll get two point eight three zero meters per second and that is what we’ll substitute it for ‘Viy’ there so that means that the Y-component final velocity is the square root of two point eight three zero meters per second squared plus two times nine point eight meters per second squared, acceleration due to gravity, times ten meters and this gives us fourteen point two eight meters per second final Y-component of the velocity. And the final velocity itself we use Pythagoras theorem and we have the X-component and we have the Y-component so we’ll take the sum of the squares and then square root and this gives us square root of four point nine zero one meters per second plus fourteen point two eight meters per second also squared and this gives us fifteen meters per second as the final velocity when the chunk of snow hits the ground.