VIDEO TRANSCRIPT

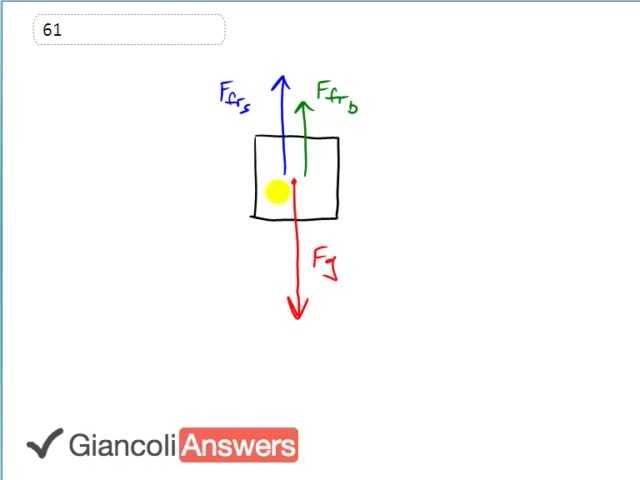
We’ll draw this rock climber as a box and show all the forces that are acting on him. There are two friction forces upwards, one is the contact between his shoes and the rock wall, and the other is the friction between his back and the other side of the chimney and then there is one force downward due to gravity. There’s also the normal forces which are resulting in the friction forces and they are equal magnitudes, otherwise he would be accelerating into one rock wall or into the other rock wall. He’s between two rock walls so he’s not obviously not going to accelerate sideways so this is the reason why the normal forces are the same in both directions. We know some more information, we know that his mass is seventy five kilograms, the coefficient of friction with his shoes is zero point eight zero and the coefficient of friction with his back is zero point six zero, and I drew the shoe friction arrow a little bit longer to represent this higher coefficient of friction between his shoe and the wall. We know that the total up forces due to the two friction forces has to equal the gravity downwards in order for him to stay stationary and that means the friction force with his shoes plus the friction force with his back has to equal ‘m’ times ‘g’ which is gravity downwards. And we’ll come up with expressions for each of these friction forces and then substitute them into that equation. Friction force with his shoe is ‘μs’ times ‘FN’ and friction force with his back is ‘μb’ times ‘FN’ and these ‘FN’s don’t need shoe or back subscripts since they are equal magnitudes. Substituting into this equation, so it becomes: ‘μs’ times ‘FN’ plus ‘μb’ times ‘FN’ equals ‘m’ times ‘g’. And your job is to figure out what is this normal force we can see that it factors out: ‘FN’ times ‘μs’ plus ‘μb’ equals ‘m’ times ‘g’. And then we can divide both sides by the total coefficient of frictions so we have the normal force equals ‘m’ times ‘g’ divided by ‘μs’ plus ‘μb’ and that is seventy five kilograms times nine point eight newtons per kilogram divided by zero point eight plus zero point six and this gives a normal force of five hundred and thirty newtons or five point three times ten raised to power two newtons. In the 5th Edition, the mass is seventy kilograms instead of seventy five and so the normal force in the 5th Edition is four point nine times ten raised to power two Newtons.