VIDEO TRANSCRIPT

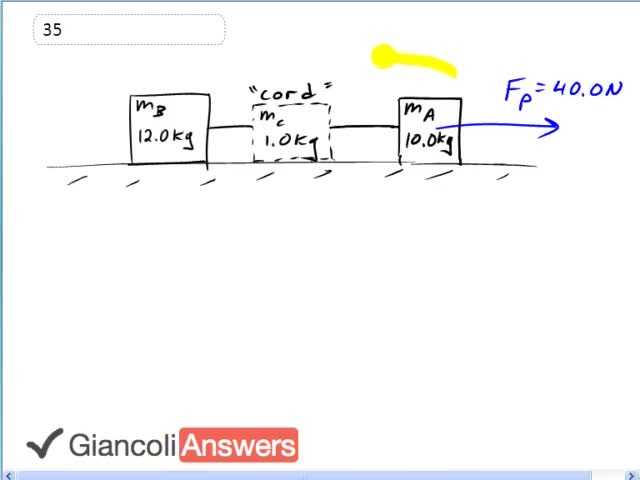
We can model these two boxes attached by a cord which does have some mass as three boxes put together with connecting cords that have no mass, so we will imagine that the massive cord is a box of mass one kilogram. Now we have to find the acceleration of this whole system and from the perspective of ‘Fp’ we can think of this system as one big box of mass ‘ma’ plus ‘mb’ plus ‘mc’ and a single force ‘Fp’ That’s the system from the perspective of force ‘Fp’ and we’ll say that that force is going to be the ‘Fp’ is going to be mass times acceleration because it’s the only force, the gravity and the normal force and important here, so it’s the total mass times acceleration and then acceleration is divided both sides by the mass, giving us: ‘a’ equals ‘Fp’ divided by the total mass so that is forty point zero newtons, divided by twelve kilograms plus ten kilograms plus one kilogram that is one point seven three nine one which we’ll round to three significant figures, one point seven four metres per second squared is the acceleration of all three parts because they accelerate together as a system. We have to find the tension force acting on block b, so the tension at the left end of the cord. So we’ll draw that box mass ‘mb’ and there’s a force to the right, this is the force on block b due to the tension ‘FbT’ and that single force is going to equal mass times acceleration: ‘FbT’ equals ‘mb’ times acceleration, and it’s mass is twelve point zero kilograms and the acceleration one point seven three nine one metres per second squared giving us a force of twenty point nine newtons. For mass ‘ma’ we know that the picture should look like this, it’s going to have the pulling force to the right and it will have some tension to the left, that’s the force on a due to the tension, which by the way is the tension in the cord at the right hand side. So it’s the tension here that we are solving for now and we will say that the force to the right minus the force to the left is: ‘ma’ times acceleration, we have to solve for ‘FAT’ and that equals ‘Fp’ minus ‘ma’ times ‘a’, simplifying: the tension of the cord near block a is going to be, substituting in numbers: forty point zero newtons minus ten kilograms times one point seven three nine one metres per second squared, this gives you twenty two point six newtons as the tension on the right hand side of the cord.