VIDEO TRANSCRIPT

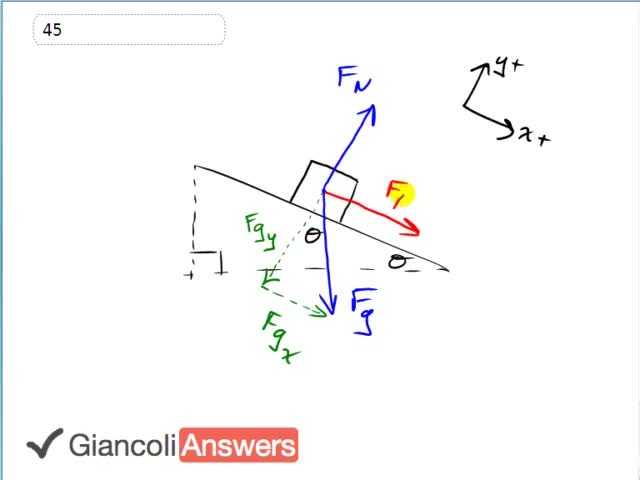
So what pushing force is needed to get this bobsled to go down a six degree slope so that it achieves a certain speed after a certain distance? Let’s get some more force vectors on our picture: we have friction opposing the motion down the ramp, we have pushing force which is longer than the friction which is going to accelerate it down the ramp, and we have gravity straight down which has some Y-component and we have the normal force perpendicular to the surface equal to the Y-component of gravity because it is not accelerate perpendicular to the surface. We’ve chosen our coordinate system so that the X-direction is positive down the ramp and we have the mass of the bob sledge is twenty two kilograms, the coefficient of kinetic friction with the ice is zero point one and theta is six degrees. Now the final speed should be sixty kilometres per hour times one hour for every three thousand six hundred seconds times one thousand metres per kilometre gives us a final speed of sixteen point six six seven metres per second and this has to happen over a distance of seventy five metres, it has to get from speed zero to speed sixteen and two thirds within seventy five metres. So we are going to first find out what acceleration is that and then based to that acceleration figure out what net force is required and then from that determine the pushing force. So find acceleration, we’ll use the formula ‘vf2’ equals ‘vi2’ plus two ‘a’ times‘d’, ‘vi’ being zero and then we’ll solve for ‘a’ by dividing both sides by two‘d’: ‘a’ equals ‘vf2’ over two‘d’ and that equals sixteen point six six seven metres per second squared over two times seventy five metres giving us an acceleration of one point eight five one nine metres per second squared. And now we’ll find the pushing force which is the whole question. We know that the pushing force is acting along with the X-component of gravity, you can see that from the picture, the pushing force is down the ramp and X-component of gravity also is down the ramp, so they both get a plus sign since positive is down the ramp and then the friction force is opposing those two, so minus friction force. All of that has to equal mass times acceleration because this is the net force on the left side. The X-component of gravity is: ‘m’ times ‘g’ times sine theta because this X-component of gravity is the opposite leg of this gravity force triangle, gravity being ‘m’ times ‘g’ opposite leg you find with sine and then the friction force is our next target. We are going to say that it is coefficient of kinetic friction times ‘FN’, ‘FN’ being equal to the Y-component of gravity and the Y-component of gravity is ‘m’ times ‘g’ cosine theta. So this normal force has to equal the Y-component of gravity and this is the adjacent leg of the gravity force triangle end so we use cosine to get that. And then we substitute for each of these into this Newton’s second law formula, the net force formula. We’ll say: ‘Fp’ equals ‘m’ times ‘a’ plus force of friction minus X-component of gravity, so we have ‘m’ times ‘’ plus ‘µk’ times ‘m’ times ‘g’ cosine theta, that’s the friction term, minus ‘m’ times ‘g’ sine theta, that’s the gravity term. simplify that by factoring out the ‘m’, we have: ‘m’ times ‘a’ plus ‘µk’ times ‘g’ cosine theta minus ‘g’ sine theta and then putting in numbers we have: twenty two kilograms times one point eight five one nine metres per second squared plus zero point one times nine point eight metres per second squared times cosine of six degrees minus nine point eight metres per second squared times the sine of six degrees and all of that works out to thirty nine point six five newtons which we’ll round to two significant figures, forty newtons is the pushing force, which is actually not that much, it’s the proximate force for lifting four kilograms which is eight pounds.