VIDEO TRANSCRIPT

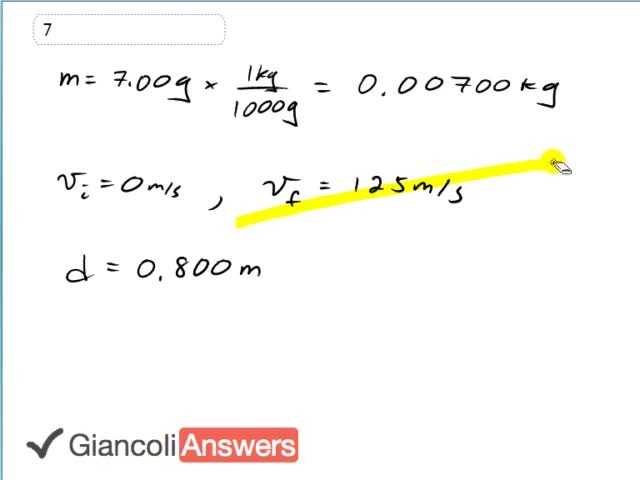
The seven gram bullet is going to accelerate from rest up until one hundred and twenty five meters per second in the 6th edition over the length of the gun barrel of point eight meters. You should always start by drawing a free body diagram although in this question it's not that crucial. It's just nice to do it as a matter of habit. You can see that there's only one horizotal force. We'll call it 'Fp' for "push". How much force does it need to get shot out of the barrel with this speed. And there's no friction, we assume. So we use the formula 'Fp' equals 'ma' because 'Fp' is the net force, since it's the only force horizontally. And our job then is to figure out the acceleration using the information given to us and then substitute that acceleration in here to get our answer. So find acceleration... we're going to use 'vf' squared equals initial velocity squared plus two 'ad'. The initial velocity being zero so that term disappears, and then we can divide both sides by two 'd' to solve for 'a'. So we have acceleration is 'vf' squared over two 'd' which is one hundred twenty five meters per second all squared, divided by two times point eight meters. Giving an acceleration of nine thousand seven hundred sixty five point six meters per second squared. And then we can substitute that into our force formula. So the mass in kilograms is point zero zero seven zero zero kilograms times nine thousand seven hundred sixty five point six meters per second squared gives us a pushing force of sixty eight point four Newtons in the 6th Edition. In the 5th Edition the final of the bullet is one hundred seventy five meters per second, and the distance is point seven zero zero meters. You might notice that these numbers are all unrealistic because a bullet goes faster than the speed of sound, and the speed of sound is three hundred and forty meters per second. It's just always nice to have a sense of whether things are realistic. Usually you look at your answer to a question and ask if it's realistc. It's also just useful to look at the question to see if it's realistic too. One hundred seventy five meters per second goes there, point seven zero zero meters goes there. Acceleration for the 5th Edition is twenty one thousand eight hundred seventy five which we'll substitute here giving a 5th edition answer of one hundred fifty three Newtons.